- 真题试卷
- 模拟试卷
- 预测试卷
1. 若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知m、n、l1、l2表示直线,α、β表示平面.若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 直角坐标系



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 正四面体的内切球,与各棱都相切的球,外接球的半径之比为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 由正数组成的等比数列{an}中,a1+a2=1,a3+a4=4,则a5+a6=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 甲乙两人独立地解决同一问题,甲解决的概率为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知点P是以F1,F2为焦点的椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获利5万元,每吨乙产品可获
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设集合








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 函数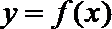
①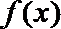
②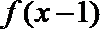
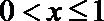
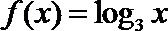
则方程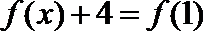
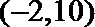
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知P是抛物线y2=4x上一个动点,Q为圆x2+(y-4)2=1上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知集合
①若

②若

③若

④若


其中所有正确命题的序号是__________。(填上所有正确命题的序号)
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知函数f(x)=
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知双曲线C的两条渐近线过坐标原点,且与以点



(1)求双曲线的方程;
(2)当

(3)当



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知锐角△ABC三个内角为A、B、C,向量

(1)求角A.
(2)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人.现采用分层抽样的方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.
(1)求从甲组抽取的工人中恰有1名女工人的概率;
(2)记ξ表示抽取的3名工人中男工人数,求ξ的分布列及数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
(1)证明:PN⊥AM.
(2)若平面 PMN与平面ABC所成的二面角为45°,试确定点P的位置.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 
(1)求函数
(2)若

(3)证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 









(1)求函数
(2)设

(3)若(2)中数列




正确答案
解析
解析已在路上飞奔,马上就到!

































