- 真题试卷
- 模拟试卷
- 预测试卷
5.某同学设计下面的程序框图用以计算和式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设x,y满足约束条件
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知椭圆








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.为了了解一片
正确答案
30
解析
解析已在路上飞奔,马上就到!
知识点
4.将一颗骰子投掷两次分别得到点数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设

①若

②若

③若

④若

其中,所有真命题的序号是( )
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,边长为1的正方形





正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数





正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
14.若直角坐标平面内的两个不同点

① 


② 



(注:点对

已知函数
正确答案
2对
解析
解析已在路上飞奔,马上就到!
知识点
11.已知








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,在梯形ABCD中,AD//BC,AC、BD相交于O,记△BCO、 △CDO、△ADO的面积分别为S1、S2、S3,则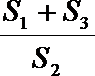
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元。如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元)。设购买某商品得到的实际折扣率=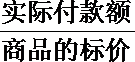
(1)写出当x∈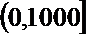
(2)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知点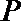
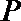
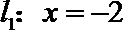
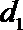
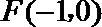
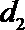
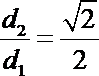
(1)求动点P所在曲线C的方程;
(2)直线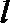
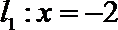
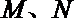
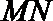
(3)记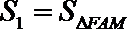
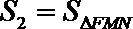
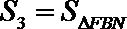
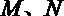
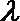
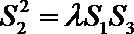
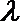
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,四棱锥







(1)求证:

(2)




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足:S=3n2an+S,an≠0,n≥2,n∈N*
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使aM时,数列{an}是递增数列。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,在四棱锥









(1)求证:平面

(2)求平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.某品牌汽车的4S店,对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
(1)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位彩用分3期付款”的概率P(A);
(2)4S店销售一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.用


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.选做题:在A、B、C、D四小题中只能选做2题。解答应写出文字说明、证明过程或演算步骤。
B.(选修4-2:矩阵与变换)
二阶矩阵M有特征值λ=8,其对应的一个特征向量

C.(选修4-4:坐标系与参数方程)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标系为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数


(1)求

(2)在锐角





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数

(1)若


(2)若




正确答案
解析
解析已在路上飞奔,马上就到!