- 真题试卷
- 模拟试卷
- 预测试卷
6.下列四个命题中真命题的个数是 ( )
①若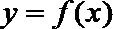

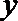
②若

③若函数

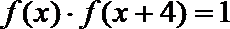

④命题“在斜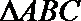

⑤命题“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知半径为5的球O被互相垂直的两个平面所截,得到的两个圆的公共弦为4,若其中的一圆的半径为4,则另一圆的半径为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若某几何体的三视图(单位:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设集合





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知复数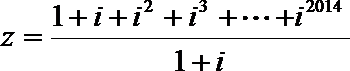
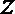
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若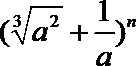
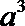
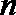
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知定义的R上的偶函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若框图所给的程序运行结果为

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
15.函数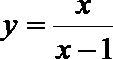
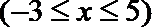
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16.已知







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 在平面区域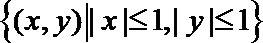
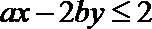
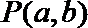
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
请在第22、23、24三题中任选一题作答。
22.选修4-1:几何证明选讲
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(Ⅰ)求证:
(Ⅱ)若

23.选修4-4:坐标系与参数方程
已知极点为直角坐标系的原点,极轴为





(Ⅰ)求直线
(Ⅱ)求点


24.选修4-5:不等式选讲
关于

(Ⅰ)当
(Ⅱ)设函数


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
18.某中学有6名爱好篮球的高三男生,现在考察他们的投篮水平与打球年限的关系,每人罚篮10次,其打球年限与投中球数如下表:
(Ⅰ)求投中球数

(Ⅱ)现在从高三年级大量男生中调查出打球年限超过



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.将函数


(Ⅰ)求数列
(Ⅱ)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱柱






(Ⅰ)求证:

(Ⅱ)求锐二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆的焦点坐标是



(Ⅰ)求椭圆的标准方程;
(Ⅱ)过


正确答案


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)当


(Ⅱ)当





(III)若对任意的



正确答案

解析
解析已在路上飞奔,马上就到!