- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
{-1}
解析
解析已在路上飞奔,马上就到!
知识点
4.函数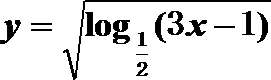
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
3.已知正方形ABCD的边长为1,点E是AB边上的动点,则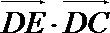
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
5.一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)骰子四个面上分别标有1,2,3,4这四个数字,抛掷这颗正四面体骰子,观察抛掷后能看到的数字。若连续抛掷两次,两次朝下面上的数字之积大于6的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在
正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
8.阅读下图所示的程序框图,运行相应的程序,输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在平面直角坐标系中,两条平行直线的横截距相差20,纵截距相差15,则这两条平行直线间的距离为( )
正确答案
12
解析
解析已在路上飞奔,马上就到!
知识点
10.已知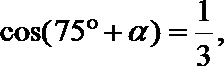

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 给出下列四个命题:
①“k =1”是“函数

② 函数


③ 函数
④ 设O是△ABC内部一点,且
其中真命题的序号是( )(写出所有真命题的序号)。
正确答案
④
解析
解析已在路上飞奔,马上就到!
知识点
14. 如图,用一块形状为半椭圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.数列




正确答案
470
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设集合W由满足下列两个条件的数列
① 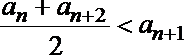
② 存在实数M,使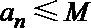
(1)在只有5项的有限数列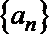
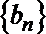



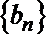
(2)设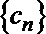
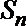

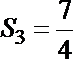

(3)设数列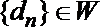



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在平面直角坐标系xOy中,椭圆C:



(1)求椭圆C的方程;
(2)判断线段PQ的垂直平分线是否经过一个定点,若定点存在,求出定点坐标;若不经过定点,请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若



(2)若对任意


(3)在(1)的条件下,设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设点P(1,0),Q(0,1)在矩阵


(1)求实数
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆





(1)求直线

(2)求点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图:在平面直角坐标系中,锐角

(1)若A、B两点的纵坐标分别为


(2)已知点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2。
(1)求证:A1C⊥平面BCDE;
(2)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.建造一条防洪堤,其断面为等腰梯形,腰与底边成角为


(1)求外周长的最小值,并求外周长最小时防洪堤高h为多少米?
(2)如防洪堤的高限制在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.设
(1)求证:
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.甲、乙两班各派三名同学参加青奥知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是

(1)用X表示甲班总得分,求随机变量X的概率分布和数学期望;
(2)记“两班得分之和是30分”为事件A,“甲班得分大于乙班得分”为事件B,求事件A,B同时发生的概率。
正确答案
解析
解析已在路上飞奔,马上就到!