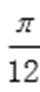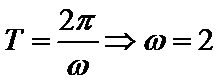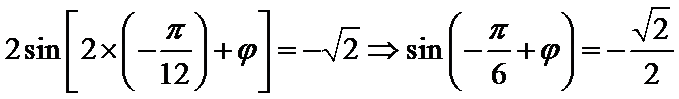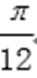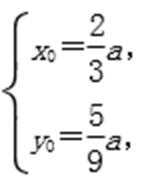- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合A={x|-2<x<0},B={x|-1<x<1},则A∪B= .
正确答案
{x|-2<x<1}
解析
直接画出数轴,画出集合A和集合B,求出并集{x|-2<x<1}
考查方向
解题思路
先画出数轴,然后求并集
易错点
本题易在集合运算中对交集与补集概念理解错误;
知识点
2.若复数z=(1+mi)(2-i)(i是虚数单位)是纯虚数,则实数m的值为 .
正确答案
-2
解析
∴
考查方向
解题思路
先化简复数Z,根据复数纯虚数概念列出方程组求出m
易错点
本题易在对复数纯虚数的概念理解不透;
知识点
3.将一骰子连续抛掷两次,至少有一次向上的点数为1的概率是 .
正确答案
解析
由题意知本题是一个等可能事件的概率,
∵将一颗骰子掷两次,共有6×6=36种结果,
满足条件的事件是至少出现一次6点向上的结果有5+5+1=11种结果,
∴至少出现一次点数6的概率是
考查方向
解题思路
将一颗骰子掷两次,共有6×6种结果,满足条件的事件是至少出现一次6点向上的结果有5+5+1种结果,得到概率.
易错点
本题列举出所有事件
知识点
6.设公差不为0的等差数列

正确答案
19
解析
设首项为

∴
考查方向
解题思路
利用基本量法解不等式组,解出首项和公差,表示a10即可
易错点
运用基本量解题,计算容易出现错误
知识点
8.已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<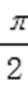
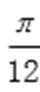
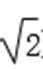
正确答案
-
解析
由题意可知:函数f(x) 的最小正周期为π,
∵它的图象过点(-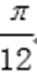
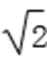
∴
∵|φ|<
Φ=-
考查方向
解题思路
根据最小正周期为π,利用周期公式即可求出ω的值,利用图象经过点(-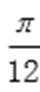
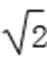
易错点
把点的坐标代入到解析式求φ,一定要注意结合其范围求解
知识点
9.已知函数f(x)=
正确答案
[-4,2]
解析

当

∴不等式f(x)≥-1的解集是[-4,2]
考查方向
解题思路
分段求出解集,然后求出并集.
易错点
在分段求解集时,一定注意范围,最后是取并集而不是交集
知识点
10.在平面直角坐标系xOy中,抛物线y2=2px(p>0) 的焦点为F,双曲线
正确答案
y=±2x
解析
抛物线y2=2px(p>0)的焦点为F
双曲线

代入抛物线的方程,可得A
由A,B,F三点共线,可得:
考查方向
解题思路
求得抛物线的焦点,双曲线的渐近线方程,代入抛物线的方程可得A,B,再由A,B,
F共线,可得
易错点
混淆抛物线和双曲线的几何性质,同时计算容易出现错误
知识点
4.如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若 一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为 .
正确答案
9
解析
日销售量不少于150的频率:
考查方向
解题思路
先计算出日销售量不少于150的频率,然后求出其对应的天数
易错点
本题易对频率分布直方图理解不透,其每个矩形面积就是频率
知识点
5.执行如图所示的流程图,则输出的k的值为 .
正确答案
5
解析
当k=1,S=1时,进入循环,S=
S=
S=
S=
考查方向
解题思路
按照程序框图的流程写出前几次循环的结果,并判断每一次得到的结果是否满足判断框中的条件,直到满足条件,执行输出
易错点
读不懂程序框图,特别是循环结构
知识点
7.如图,正三棱柱ABC—A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A—A1EF的体积是 .
正确答案
解析
∵
过

∴
在
∵
∴E点到面


∴
考查方向
解题思路
先转化








易错点
不会用运用转化化归思想,把三棱锥A—A1EF的体积转化为三棱锥E—AA1F体积
知识点
11.在△ABC中,A=120°,AB=4.若点D在边BC上,且


正确答案
3
解析
△ABC中,∠BAC=120°,AB=4,点D在边BC上,

∴
∴
两边同时平方可得:
解得

考查方向
解题思路
画出图形,结合图形,利用


面向量的数量积求出
易错点
利用向量求

知识点
12.已知圆O:x2+y2=1,圆M:(x-a)2+(y-a+4)2=1.若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,则实数a的取值范围为 .
正确答案
[2-

解析
如图,
圆O的半径为1,圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使
得∠APB=60°,则∠APO=30°,在Rt△PAO中,PO=2,
又圆M的半径等于1,圆心坐标M(a,a-4),
∴|PO|min=|MO|-1,|PO|max=|MO|+1,
∵
∴
∴解得实数a的取值范围为[2-

考查方向
解题思路
由题意画出图形,利用两点间的距离关系求出OP的距离,再由题意得到关于a的不
等式求得答案.
易错点
不会利用数形结合画出图形,找出OP的距离的不等关系
知识点
13.已知函数f(x)=ax2+x-b(a,b均为正数),不等式f(x)>0的解集记为P,集合Q=
{x|-2-t<x<-2+t}.若对于任意正数t,P∩Q≠,则
正确答案
解析
∵已知函数f(x)=ax2+x-b(a,b均为正数),不等式f(x)>0的解集记为P,集合Q=
{x|-2-t<x<-2+t}.若对于任意正数t,P∩Q≠,
∴-2∈P,即f(-2)≥0,则4a-2-b≥0,即
又由题意知,
∴
考查方向
解题思路
根据不等式解集对应的关系,得到-2∈P,然后利用基本不等式进行求解即可
易错点
找不出不等关系f(-2)≥0,同时注意基本关系式适用条件
知识点
14.若存在两个正实数x、y,使得等式x+a(y-2ex)(lny-lnx)=0成立,其中e为自然对数的底数,则实数a的取值范围为 .
正确答案
a<0或a≥
解析
∵x+a(y-2ex)(lny-lnx)=0成立
∴
设
即
设

即当t=e时,函数g(t)取得极小值,为g(e)=(e-2e)lne=-e,即g(t)≥g(e)=-e,
若
∴a<0或a≥
考查方向
解题思路
根据函数与方程的关系将方程进行转化,利用换元法转化为方程有解,构造函数求函
数的导数,利用函数极值和单调性的关系进行求解即可.
易错点
能成立问题要转化有解问题,同时要构造函数求最值,同时计算容易出现错误
知识点
已知α为锐角,cos(α+

15.求tan(α+
16.求sin(2α+
正确答案
(1)2 ;
解析
解:(1)因为α∈(0,



所以sin(α+


所以tan(α+

考查方向
解题思路
本题考查三角恒等变换,解题步骤如下:
1)利用平方关系求出sin(α+

2)利用已知角表示未知角sin(2α+



易错点
忽略角的范围取值和角与角的关系
正确答案
(2)
解析
解:
(2)因为sin(2α+




cos(2α+



所以sin(2α+







考查方向
解题思路
本题考查三角恒等变换,解题步骤如下:
1)利用平方关系求出sin(α+

2)利用已知角表示未知角sin(2α+



易错点
忽略角的范围取值和角与角的关系
对于函数f(x),在给定区间[a,b]内任取n+1(n≥2,n∈N*)个数x0,x1,x2,…,xn,使得
a=x0<x1<x2<…<xn-1<xn=b,记S=
22.若函数f(x)=-2x+1,给定区间为[-1,1],求S的值;
23.若函数f(x)=
24.对于给定的实数k,求证:函数f(x)=klnx-
正确答案
(1)4;
解析
(1)解:因为函数f(x)=-2x+1在区间[-1,1]为减函数,
所以f(xi+1)<f(xi),所以|f(xi+1)-f(xi)|= f(xi)-f(xi+1).
S=
=f(x0)-f(xn)=f(-1)-f(1)=4.
考查方向
解题思路
本题考查函数恒成立问题,解题步骤如下:
1)先通过f(x)=-2x+1的单调性,直接求出|f(xi+1)-f(xi)|= f(xi)-f(xi+1)代入即可求出;
易错点
不会转化
正确答案
(2)
解析
(2) 解:由f′(x)=
当x<1时,f′(x)>0,所以f (x)在(-∞,1)为增函数;
当x>1时,f′(x)<0,所以f (x)在(1,+∞)为减函数;
所以f (x)在x=1时取极大值
设xm≤1<xm+1,m∈N,m≤n-1,
则S=
=|f(x1)-f(0)|+…+|f(xm)-f(x m-1)|+|f(xm+1)-f(x m)|+|f(xm+2)-f(x m+1)|+…+|f(2)-f(x n-1)
=[f(x1)-f(0)]+…+[f(xm)-f(x m-1)]+|f(xm+1)-f(x m)|+[f(xm+1)-f(x m+2)]+…+[f(xn-1)-f(2)]
=[f(xm)-f(0)]+|f(xm+1)-f(x m)|+[f(xm+1)-f(2)].
因为|f(xm+1)-f(x m)|≤[f(1)-f(xm)]+[f(1)-f(xm+1)],当x m=1时取等号,
所以S≤f(xm)-f(0)+f(1)-f(xm)+f(1)-f(xm+1)+f(xm+1)-f(2)
=2 f(1)-f(0)-f(2)=
所以S的最大值为
考查方向
解题思路
本题考查函数恒成立问题,解题步骤如下:
2)先研究f(x)=
求出即可;
易错点
不会转化
正确答案
(3)对于给定的实数k,函数f(x)=klnx-
解析
(3)证明:f′(x)=

①当k≥e2时,k-x2≥0恒成立,即f′(x)≥0恒成立,所以f(x)在[1,e]上为增函数,
所以S=
=f(x n)-f(x0)=f(e)-f(1)=k+

因此,存在正数A=k+

②当k≤1时,k-x2≤0恒成立,即f′(x)≤0恒成立,所以f(x)在[1,e]上为减函数,
所以S=
=f(x0)-f(xn)= f(1)-f(e)= 

因此,存在正数A=

③当1<k<e2时,由f′(x)=0,得x=

当f′(x)<0,得


设xm≤
则S=
=|f(x1)-f(x0)|+…+|f(xm)-f(x m-1)|+ |f(xm+1)-f(x m)|+ |f(xm+2)-f(x m+1)|+…+|f(xn)-f(x n-1)
=f(x1)-f(x0)+…+f(xm)-f(x m-1) + |f(xm+1)-f(x m)|+ f(xm+1)-f(x m+2) +…+f(xn-1)-f(x n)
=f(xm)-f(x0) + |f(xm+1)-f(x m)| + f(xm+1)-f(x n)
≤f(xm)-f(x0) + f(xm+1)-f(x n)+ f(

=2 f(




因此,存在正数A=klnk-2k+

综上,对于给定的实数k,函数f(x)=klnx-
考查方向
解题思路
本题考查函数恒成立问题,解题步骤如下:
3)先研究函数f(x)=klnx-
易错点
不会转化
在平面直角坐标系xOy中,点C在椭圆M: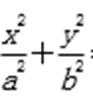
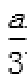
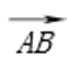
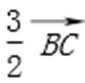
20.求椭圆M的离心率;
21.设椭圆M的焦距为4,P,Q是椭圆M上不同的两点,线段PQ的垂直平分线为直线l,且直线l不与y轴重合.
①若点P(-3,0),直线l过点(0,-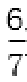
②若直线l过点(0,-1) ,且与x轴的交点为D,求D点横坐标的取值范围.
正确答案
(1)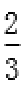
解析
解:(1)设C (x0,y0),则
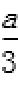
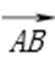
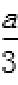
因为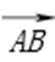
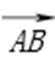
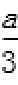
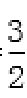
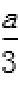

得
代入椭圆方程得a2=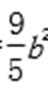
因为a2-b2=c2,所以e=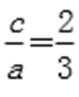
考查方向
解题思路
本题考查直线与椭圆位置关系,解题步骤如下:
(1)设C(m,n),由向量共线的坐标表示,可得C的坐标,代入椭圆方程,可得a,b的关系,
再由离心率公式计算即可得到所求值;
(2)①由题意可得c=2,a=3, b2=5,可得椭圆方程,设直线PQ的方程为y=k(x+3),代入椭圆方程,运用韦达定理和中点坐标公式,再由两直线垂直的条件:斜率之积为-1,解方程可得k,进而得到所求直线方程;
②设直线PQ的方程为y=kx+m,代入椭圆方程可得,运用韦达定理和中点坐标公式,再由两直线垂直的条件,求得4m=5+9k2,再由中点在椭圆内,可得k的范围,再由直线l的方程可得D的横坐标的范围.
易错点
第二问容易计算错误
正确答案
(2)①y=-x+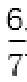

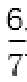
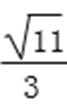
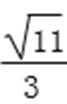
解析
解:(2)①因为c=2,所以a2=9,b2=5,所以椭圆的方程为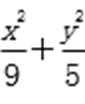
设Q (x0,y0),则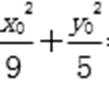
因为点P(-3,0),所以PQ中点为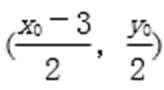
因为直线l过点(0,-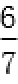
所以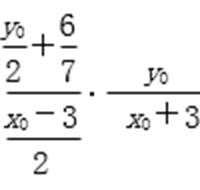
化简得x02=9-y02-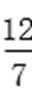
将②代入①化简得y02-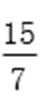
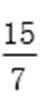
将y0=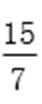
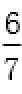
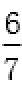
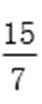
所以PQ斜率为1或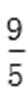
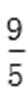
所以直线l的方程为y=-x+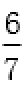
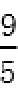
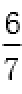
②设PQ:y=kx+m,则直线l的方程为:y=-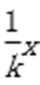
将直线PQ的方程代入椭圆的方程,消去y得(5+9k2)x2+18kmx+9m2-45=0.…………①,
设P(x1,y1),Q(x2,y2),中点为N,
xN=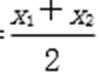
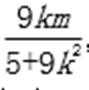
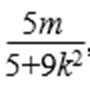
代入直线l的方程得9k2=4m-5. ……②
又因为△=(18km)2-4(5+9k2) (9m2-45)>0,
化得m2-9k2-5<0.
将②代入上式得m2-4m<0,解得0<m<4,
所以-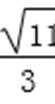
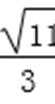
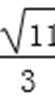
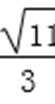
综上所述,点D横坐标的取值范围为(-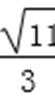
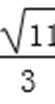
考查方向
解题思路
本题考查直线与椭圆位置关系,解题步骤如下:
(1)设C(m,n),由向量共线的坐标表示,可得C的坐标,代入椭圆方程,可得a,b的关系,
再由离心率公式计算即可得到所求值;
(2)①由题意可得c=2,a=3, b2=5,可得椭圆方程,设直线PQ的方程为y=k(x+3),代入椭圆方程,运用韦达定理和中点坐标公式,再由两直线垂直的条件:斜率之积为-1,解方程可得k,进而得到所求直线方程;
②设直线PQ的方程为y=kx+m,代入椭圆方程可得,运用韦达定理和中点坐标公式,再由两直线垂直的条件,求得4m=5+9k2,再由中点在椭圆内,可得k的范围,再由直线l的方程可得D的横坐标的范围.
易错点
第二问容易计算错误
如图,在三棱锥P—ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.
17.求证:PB∥平面MNC;
18.若AC=BC,求证:PA⊥平面MNC.
正确答案
见解析
解析
证:(1)因为M,N分别为AB,PA的中点,
所以MN∥PB.
因为MN平面MNC,PB平面MNC,
所以PB∥平面MNC.
考查方向
解题思路
本题考查线面平行的判定,面面垂直的性质和线面垂直,解题步骤如下:
(1)根据中位线定理可得MN∥PB,故而PB∥平面MNC.
(2)由三线合一可得CM⊥AB,再有面面垂直得出CM⊥平面PAB,故CM⊥PA,由AP⊥PB,MN∥PB可得PA⊥MN,故而PA⊥平面MNC.
易错点
线面平行和线面垂直判定定理记不熟,不会灵活运用
正确答案
见解析
解析
证: (2)因为PA⊥PB,MN∥PB,所以PA⊥MN.
因为AC=BC,AM=BM,所以CM⊥AB.
因为平面PAB⊥平面ABC,CM平面ABC,平面PAB∩平面ABC=AB,
所以CM⊥平面PAB.
因为PA平面PAB,所以CM⊥PA.
因为PA⊥MN,MN平面MNC,CM平面MNC,MN∩CM=M,
所以PA⊥平面MNC.
考查方向
解题思路
本题考查线面平行的判定,面面垂直的性质和线面垂直,解题步骤如下:
(1)根据中位线定理可得MN∥PB,故而PB∥平面MNC.
(2)由三线合一可得CM⊥AB,再有面面垂直得出CM⊥平面PAB,故CM⊥PA,由AP⊥PB,MN∥PB可得PA⊥MN,故而PA⊥平面MNC.
易错点
线面平行和线面垂直判定定理记不熟,不会灵活运用
19.如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
正确答案
当A,B两点离道路的交点都为2-
解析
解法一:如图,分别由两条道路所在直线建立直角坐标系xOy.
设A(a,0),B(0,b)(0<a<1,0<b<1),
则直线AB方程为
因为AB与圆C相切,所以
化简得 ab-2(a+b)+2=0,即ab=2(a+b)-2.
因此AB=
=
因为0<a<1,0<b<1,所以0<a+b<2,
于是AB=2-(a+b).
又ab=2(a+b)-2≤
解得0<a+b≤4-2

因为0<a+b<2,所以0<a+b≤4-2
所以AB=2-(a+b) ≥2-(4-2

当且仅当a=b=2-
所以AB最小值为2

答:当A,B两点离道路的交点都为2-
解法二:如图,连接CE,CA,CD,CB,CF.
设∠DCE=θ,θ∈(0,

在直角三角形CDA中,AD=tan
在直角三角形CDB中,BD=tan(

所以AB=AD+BD=tan


=tan

令t=tan
则AB=f(t)=t+


当且仅当t=
所以AB最小值为2
此时A,B两点离两条道路交点的距离是1-(

答:当A,B两点离道路的的交点都为2-
考查方向
解题思路
本题考查基本不等式在最值问题中的运用,解题步骤如下:
分别由两条道路所在直线建立直角坐标系xOy.设A(a,0),B(0,b)(0<a<1,0<b<1),求得直线AB的方程和圆的方程,运用直线和圆相切的条件:d=r,求得a,b的关系,再由两点的距离公式和基本不等式,解不等式可得AB的最小值,及此时A,B的位置.
易错点
读不懂题意,无法得出ab=2(a+b)-2,利用基本不等式求出最值
知识点
已知数列{an}的前n项和为Sn,且对任意正整数n都有an=(-1)nSn +pn(p为常数,p≠0).
25.求p的值;
26.求数列{an}的通项公式;
27.设集合An={a2n-1,a2n},且bn,cn
若b1≠c1,求证:对任意n∈N*,Pn≠Qn.
正确答案
(1)p=-
解析
解:(1)由a1=-S1+p,得a1=
由a2=S2+p2,得a1=-p2,所以
又p≠0,所以p=-
考查方向
解题思路
本题考查数列求通项、求和,解题步骤如下:
(1)令n=1,n=2,可得p的方程,由p不为0,可得p的值;
易错点
错位相减法容易计算错误
正确答案
(1)p=-
解析
(2)由an=(-1)nSn+(-
①+②得an+an+1=(-1)n(-an+1)+
当n为奇数时,an+an+1=an+1
所以an=-
当n为偶数时,an+an+1=-an+1+
所以an=-2an+1+
所以an=
考查方向
解题思路
本题考查数列求通项、求和,解题步骤如下:
(2)讨论n为偶数,或奇数,将n换为n-1,两式相加可得所求通项公式;
易错点
错位相减法容易计算错误
正确答案
见解析
解析
解:(3)An=
不妨设b1>0,则b1=

则Pn=b1+2b2+3b3+…+nbn≥
设S=
两式相减得


所以S<

因为Qn= c1+2 c 2+3 c 3+…+n c n≤
所以Pn≠Qn.
考查方向
解题思路
(3)求得An={a2n-1,a2n}= An=
易错点
错位相减法容易计算错误
28.如图,在Rt△ABC中,AB=BC.以AB为直径的⊙O交AC于点D,过D作DEBC,垂足为E,连接AE交⊙O于点F.求证:BECE=EFEA.
正确答案
见解析
解析
证明:连接BD.因为AB为直径,所以BD⊥AC.
因为AB=BC,所以AD=DC.
因为DEBC,ABBC,所以DE∥AB,
所以CE=EB.
因为AB是直径,ABBC,所以BC是圆O的切线,
所以BE2=EFEA,即BECE=EFEA.
考查方向
解题思路
本题考查三角函数与解三角形,解题步骤如下:
连接BD,由已知得∠BDA=90°,∠BDC=90°,DE2=BE•CE,由此利用切割线定理能证明BE•CE=EF
•BA.
易错点
切割线定理不会应用
知识点
甲、乙两人投篮命中的概率分别为与,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
31.求比赛结束后甲的进球数比乙的进球数多1个的概率;
32.设ξ表示比赛结束后甲、乙两人进球数的差的绝对值,求ξ的概率分布和数学期望E(ξ).
正确答案
(1)
解析
(1)比赛结束后甲的进球数比乙的进球数多1个有以下几种情况:
甲进1球,乙进0球;甲进2球,乙进1球;甲进3球,乙进2球.
所以比赛结束后甲的进球数比乙的进球数多1个的概率
P=
考查方向
解题思路
本题考查概率的求法,解题步骤如下:
(1)比赛结束后甲的进球数比乙的进球数多1个,有以下几种情况:甲进1球,乙进0球;甲进2球,乙进1球;甲进3球,乙进2球.由此能求出比赛结束后甲的进球数比乙的进球数多1个的概
率.
易错点
解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.
正确答案
(2)E(ξ)=1
解析
(2)ξ的取值为0,1,2,3,所以 ξ的概率分布列为
所以数学期望E(ξ)=
考查方向
解题思路
本题考查概率的求法,解题步骤如下:
(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
易错点
解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.
设(1-x)n=a0+a1x+a2x2+…+anxn,n∈N*,n≥2.
33.设n=11,求|a6|+|a7|+|a8|+|a9|+|a10|+|a11|的值;
34.设bk=

正确答案
(1)1024;
解析
解:(1)因为ak=(-1)k 
当n=11时,|a6|+|a7|+|a8|+|a9|+|a10|+|a11|=
=
考查方向
解题思路
本题考查二项式定理和性质,解题步骤如下:
(1)由二项式定理可得ak=(-1)k
=(-1)k-1 

易错点
二项式定理和性质不会熟练应用,容易计算错误
正确答案
(2)1
解析
(2)bk=


当1≤k≤n-1时,bk=(-1)k+1 





当m=0时,|

当1≤m≤n-1时,
Sm=-1+

所以|

考查方向
解题思路
本题考查二项式定理和性质,解题步骤如下:
(2)由组合数的阶乘公式可得bk= (-1)k+1 
=(-1)k-1 

易错点
二项式定理和性质不会熟练应用,容易计算错误
已知a,b是实数,如果矩阵A=
29.求a,b的值.
30.若矩阵A的逆矩阵为B,求B2.
正确答案
(1)a=-1,b=5;
解析
解:(1)由题意,得
所以a=-1,b=5.
考查方向
解题思路
本题考查矩阵变换,解题步骤如下:
(Ⅰ)根据变换的性质列出一组方程式求解出a,b;
(Ⅱ)求出|B|,即可求矩阵B的逆矩阵
易错点
容易计算错误
正确答案
(2)B2=
解析
(2)由(1),得A=

所以B2=
考查方向
解题思路
本题考查矩阵变换,解题步骤如下:
(Ⅰ)根据变换的性质列出一组方程式求解出a,b;
(Ⅱ)求出|B|,即可求矩阵B的逆矩阵
易错点
容易计算错误