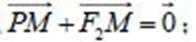- 真题试卷
- 模拟试卷
- 预测试卷
2.已知复数z满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知实数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知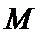
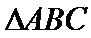
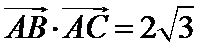
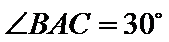
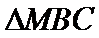
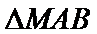
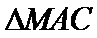
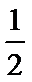
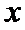
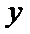
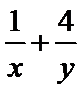
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题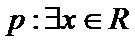
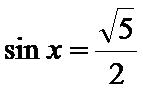
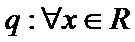
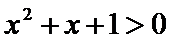
① 题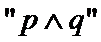
②命题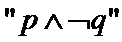
③命题
④命题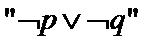
其中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数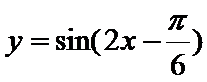

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在平面上,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球的表面积为( )
正确答案
29π
解析
解析已在路上飞奔,马上就到!
知识点
12.在


正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
14.将



正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
15.如果





①函数

②若奇函数



③若函数






④若不恒为零的函数






其中正确的是( ) (写出所有正确命题的编号).
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
13.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为________.
正确答案
30,20
解析
解析已在路上飞奔,马上就到!
知识点
17.甲乙两班进行消防安全知识竞赛,每班出






(1)求随机变量

(2)求在甲队和乙队得分之和为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
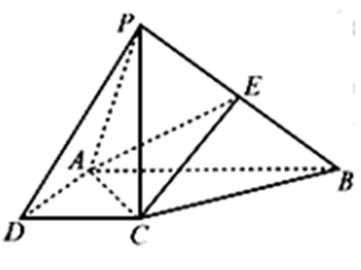
18.如图,在四棱锥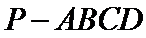
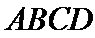
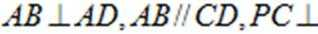
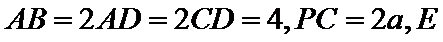

(Ⅰ)求证:平面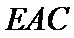

(Ⅱ)若二面角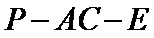
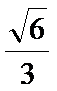
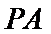
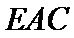
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.函数

(Ⅰ)当

(Ⅱ)当

(Ⅲ)求证:

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列




(1)求数列
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数
(Ⅰ)求函数
(Ⅱ)将函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知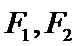
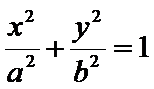
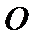
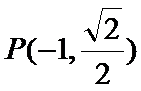
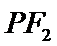
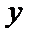
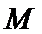
(I)求椭圆的标准方程;
(II)⊙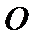
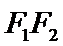
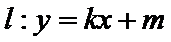
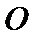
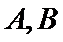
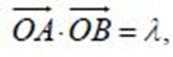
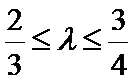
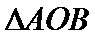
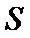
正确答案
解析
解析已在路上飞奔,马上就到!