- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 阅读程序框图,运行相应的程序,若输出
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知一个几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知椭圆










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知正四棱锥





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.将数字
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 函数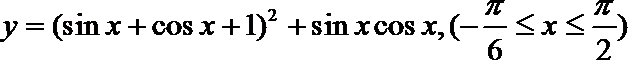
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知定义在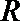

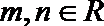
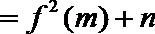
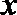
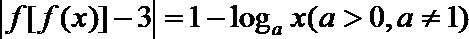
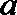
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,四棱锥




(1)若

(2)若平面







正确答案
(1)



又



又


又




(2)






以


则


所以


设平面

取
由二面角



解析
解析已在路上飞奔,马上就到!
知识点
17. 设公比大于零的等比数列







满足


(1)求数列

(2)设


正确答案
(1)由

又

则得
所以

(2)


则

即

当



解析
解析已在路上飞奔,马上就到!
知识点
18. 某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)求员工甲抽奖一次所得奖金
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数
正确答案
(1)甲抽奖一次,基本事件的总数为





(2)由(1)得乙一次抽奖中奖的概率为
四次抽奖是相互独立的,所以中奖次数
故
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,已知椭圆

(1)设

求证:动点
(2)若

的斜率之积等于直线
的面积是否为定值,说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)当


(2)如果函数









正确答案
(1)当


对于

∴
∴

(2)在区间(1,+∞)上,函数

则
令

且


∵
1) 若



当







当




2) 若



上是减函数;要使

所以

又因为h/(x)= –x+2a–

h(x)在(1, +∞)上为减函数,
h(x)<h(1)= 

所以a



解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24题中任选一题作答,如果多做,按所做的第一题计分.
22.[选修4-1:几何证明选讲]
已知:如图






(1)求证:
(2)求
23. [选修4-5:坐标系与参数方程]
已知直线






(1)求
(2)以坐标原点为极点,





24. [选修4-4:不等式选讲]
已知关于

(1)当
(2)若不等式恒成立,求
正确答案
22.(1) 


又因为:

因为:

又因为:
(2)设



⊙O的半径为


23.(1)直线


则直线



且圆


即:

(2)圆

则圆

圆

则
得到公共弦长为
24.(1)当

则:





综上:不等式的解集为
(2)
解得:
解析
解析已在路上飞奔,马上就到!