- 真题试卷
- 模拟试卷
- 预测试卷
3.下图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[20,30)内的概率为
正确答案
解析
略
知识点
4.设a=log32,b=log52,c=log23,则( ).
正确答案
解析
略
知识点
5.执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于( ).
正确答案
解析
略
知识点
2.等差数列{an}的公差为2,若a2,a4,a8成等比数列,则{an}的前n项和Sn=( )
正确答案
解析
略
知识点
9.关于




正确答案
解析
略
知识点
1.
正确答案
解析
略
知识点
6.函数f(x)在x=x0处导数存在,若p:f′(x0)=0:q:x=x0是f(x)的极值点,则( )
正确答案
解析
略
知识点
7.一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为( ).
正确答案
解析
略
知识点
8.已知抛物线C:



正确答案
解析
略
知识点
10.已知函数


正确答案
解析
略
知识点
12.已知正方形ABCD的边长为2,E为CD的中点,则
正确答案
2
解析
略
知识点
14.设



正确答案
解析
略
知识点
13.函数f(x)=sin(x+φ)﹣2sinφcosx的最大值为 。
正确答案
1
解析
略
知识点
11.设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=_____。
正确答案
解析
略
知识点
15.将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为 ________。
正确答案
解析
略
知识点
18.四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(1)求C和BD;
(2)求四边形ABCD的面积.
正确答案
见解析。
解析
(1)在△BCD中,BC=3,CD=2,
由余弦定理得:BD2=BC2+CD2﹣2BC•CDcosC=13﹣12cosC①,
在△ABD中,AB=1,DA=2,A+C=π,
由余弦定理得:BD2=AB2+AD2﹣2AB•ADcosA=5﹣4cosA=5+4cosC②,
由①②得:cosC=

(2)∵cosC=


则S=






知识点
19.设函数f(x)=alnx+
(1)求b;
(2)若存在x0≥1,使得f(x0)<
正确答案
见解析。
解析
(1)f′(x)=
∴f′(1)=a+(1﹣a)×1﹣b=0,解得b=1.
(2)函数f(x)的定义域为(0,+∞),由(1)可知:f(x)=alnx+
∴

①当a

∴函数f(x)在(1,+∞)单调递增,
∴存在x0≥1,使得f(x0)<


解得
②当

则当x∈

当x∈

∴存在x0≥1,使得f(x0)<

而


③若a>1时,f(1)=
综上可得:a的取值范围是
知识点
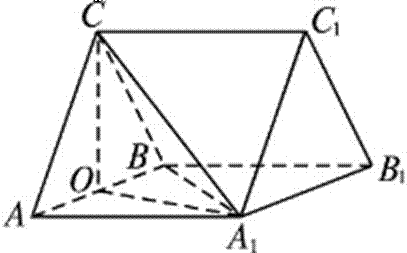
20.如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=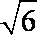
正确答案
见解析。
解析
(1)证明:取AB的中点O,连结OC,OA1,A1B.
因为CA=CB,
所以OC⊥AB.
由于AB=AA1,∠BAA1=60°,
故△AA1B为等边三角形,
所以OA1⊥AB.
因为OC∩OA1=O,所以 AB⊥平面OA1C.
又A1C⊂平面OA1C,故AB⊥A1C.
(2)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,
所以OC=OA1=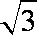
又A1C=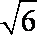
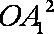
故OA1⊥OC.
因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC-A1B1C1的高.
又△ABC的面积S△ABC=
知识点
17.经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率.
正确答案
见解析。
解析
(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000.
当X∈[130,150]时,T=500×130=65 000.
所以
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
知识点
16.设数列



(1)求


(2)已知





正确答案
见解析。
解析
(1)由题设知{an}是首项为1,公比为3的等比数列,
所以an=3n-1,Sn=

(2)b1=a2=3,b3=1+3+9=13,b3-b1=10=2d,
所以公差d=5,
故T20=20×3+
知识点
21.设F1,F2分别是C:

(1)若直线MN的斜率为
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,B.
正确答案
见解析。
解析
(1)∵M是C上一点且MF2与x轴垂直,∴M的横坐标为c,当x=c时,y=

若直线MN的斜率为



则

(2)由题意,原点O是F1F2的中点,则直线MF1与y轴的交点D(0,2)是线段MF1的中点,故
由|MN|=5|F1N|,解得|DF1|=2|F1N|,设N(x1,y1),由题意知y1<0,
则


将b2=4a代入得