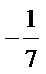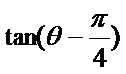- 真题试卷
- 模拟试卷
- 预测试卷
已知四棱锥








21.求证:平面
22.若点



正确答案
略
解析




又
考查方向
解题思路
先利用长度证明


易错点
无法判断哪条线垂直哪个平面导致无法证出;
正确答案
解析
以




过



则
设平面

则
取



设平面

则
由



考查方向
本题主要考查空间面面位置关系及二面角的求解,意在考查考生的空间想象能力和运算求解能力。
解题思路
建立空间直角坐标系后利用求点的坐标、线的方向向量、面的法向量,带入公式即可。
易错点
建系之后运算出错。
已知函数
25.当

26.若



正确答案
单调递增
解析





考查方向
解题思路
求导,构造分子为新函数继续求导,得到分子大于0,进而得到
易错点
不会将求导进行到底,导致求导后无法判断正负;
正确答案
略
解析



当






又




又

由(Ⅰ)知

考查方向
解题思路
先判断





易错点

在



17.求角
18.若点



正确答案
解析

即



考查方向
解题思路
先根据正弦定理将题中给出的式子全部化为角的形式,然后利用三角函数的公式求出角B;
易错点
将

正确答案
解析
解法一:取





由(Ⅰ)知

由正弦定理知,

解法二:由(Ⅰ)知



在

又

由正弦定理知,

考查方向
解题思路
先设出未知数x,然后将三角形ABC中的边AC,BC全部用x表示出来,然后利用正弦定理列出方程求出答案。
易错点
不会构造函数的思想,导致无从下手。
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外课外体育运动时间在
19.请根据上述表格中的统计数据填写下面

20.将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学



参考公式:
参考数据:
正确答案

所以在犯错误的概率不超过
解析
所以在犯错误的概率不超过
考查方向
本题主要考查统计中的独立性检验、离散型随机变量的分布列、期望和方差等知识,意在考查考生对于数据的处理能力和应用能力。
解题思路
根据题中给出数据完善列联表,求出
易错点
1.独立性检验中
2.不知道该保留小数点后几位导致扣分
正确答案
解析
由表中数据可得,抽到“课外体育达标”学生的频率为0.25,将频率视为概率,

考查方向
解题思路
先判断出随机变量服从二项分布,利用二项分布的期望和方差求出即可。
易错点
判断不出随机变量服从二项分布。
已知抛物线


23.求抛物线的方程;
24.设








正确答案
解析
设点



因为直线



所以抛物线的方程为
考查方向
本题主要考查导数的几何意义,抛物线的性质,直线与抛物线的位置关系等问题,意在考查考生的计算能力及逻辑推理能力。
解题思路
根据切线方程求出
易错点
不会联想到导数导致运算出错;
正确答案
8
解析
设线段


∴直线

即


联立
得

设



当且仅当


考查方向
本题主要考查导数的几何意义,抛物线的性质,直线与抛物线的位置关系等问题,意在考查考生的计算能力及逻辑推理能力。
解题思路
先根据题意设出直线

易错点
不会挖掘题中的隐含条件:直线
如图,在锐








27.求证:

28.若


正确答案
略
解析
连结
又
∴

而

∴
又
∴
而
∴

考查方向
解题思路
利用直径所对的圆周角是直角和三角形的中位线得到
易错点
不会根据题意正确做辅助线,导致没有头绪;
正确答案
5
解析
连


∴


由切割线定理得:
即

考查方向
解题思路
根据题意证明

易错点
找不到三角形相似的条件,进而不知道往什么方向走。
8.有6名选手参加演讲比赛,观众甲猜测:4号或5号选手得第一名;观众乙猜测:3号选手不可能得第一名;观众丙猜测:1,2,6号选手中的一位获得第一名;观众丁猜测:4,5,6号选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )
正确答案
解析
若甲猜对,则4号或5号选手得第一名,那么乙也猜对了,不符合题意,所以甲没猜对,得第一名的是1,2,3或6号,若乙猜对,则1,2或6号得了第一名,那么丙也猜对了,所以乙没有猜对,3号没有得第一,所以得第一的是3号,所以丙也没猜对,丁猜对了,故选D。
考查方向
解题思路
逐个人去分析他所猜结果的正确性。
易错点
1.不知道从什么地方入手解决;
2.从某个观众猜起,由于信息比较多,导致混乱。
知识点
12.已知直线





正确答案
解析
设


由曲线


化简得:

所以
即
而点A,B在曲线
所以
所以

即
所以
将

解得
考查方向
解题思路
1.先根据曲线在A,B处的切线平行得到
2.将点A,B的坐标带入直线和曲线方程中消元、相加得到所要的关于p的方程求解即可。
易错点
1.题中给出的条件多无从下手;
2.不会想到将两式相加构造等式,这是本题最大的难点部分,不容易突破。
知识点
1.已知集合

正确答案
解析
由题意得,集合

考查方向
本题主要考查集合的基本运算、集合间的基本,意在考查考生的运算能力,数形结合的能力。
解题思路
1.先求集合A,B;
2.然后利用数轴求出
易错点
对于集合B,易错求成
知识点
2.若复数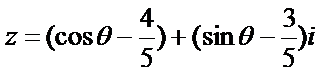
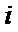
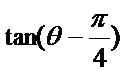
正确答案
解析
由题意得,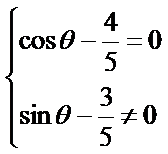
所以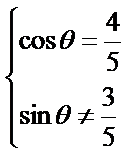
所以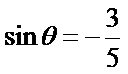
所以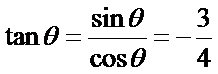
所以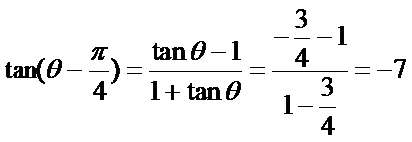
故选A。
考查方向
本题主要考查复数的概念、同角三角函数的基本关系、两角和与差的三角函数等知识,意在考查考生的运算能力和逻辑推理能力。
解题思路
1.先根据条件求出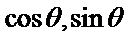
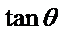
2.根据两角差的正切公式求出
易错点
对于纯虚数的概念理解不好,不注意虚部不为0,导致误选D;
知识点
3.在各项均为正数的等比数列



正确答案
解析
由







考查方向
本题主要考查数列的通项公式、等差中项、前n项和等知识,意在考生的运算推理能力。
解题思路
1.先根据

2.然后利用等比数列的求和公式求出
易错点
1.不会转化
2.误用等差数列求等比数列的前n项和。
知识点
4.已知函数




正确答案
解析
由题意得













考查方向
本题主要考查三角函数的图像和性质、诱导公式等知识,意在考查考生对于三角函数基础知识的掌握程度。
解题思路
1.先根据题中条件求出函数
2.然后利用对称中心的坐标公式求出此函数的对称中心。
易错点
1.图像平移时容易错写成
2.混淆对称中心与对称轴导致结果出错。
知识点
10.已知变量




正确答案
解析
由









考查方向
本题主要考查线性规划的有关知识,意在考查考生数形结合、分类讨论的数学思想。
解题思路
1.先做出约束条件对应的可行域;
2.求出可行域端点的坐标,将各个点带入目标函数求出a之后验证是否能在该点取到最大值即可。
易错点
1.容易将顶点带入求出a之就选,不验证是否在该点取到最大值;
2.可行域画错导致后面出错。
知识点
5.甲、乙、丙、丁、戊五位同学站成一排照相留念,则在甲乙相邻的条件下,甲丙也相邻的概率为( )
正确答案
考查方向
易错点
1.不会求甲乙相邻的排法有多少种;
知识点
7.若如下框图所给的程序运行结果为S=41,则图中的判断框①中应填入的是( )
正确答案
解析







考查方向
解题思路
根据给出的程序框图循环执行,直到求出S=41跳出循环,此时i=5.
易错点
无法确定程序结束的条件导致出错,容易误选A。
知识点
9.设





正确答案
解析
由题意知,








考查方向
本题主要考查椭圆的定义、几何性质等知识,意在考查考生的运算求解和分析问题、解决问题的能力。
解题思路
1.先求出椭圆中的基本量;
2.根据题中条件判断出P点在通径上,得到

易错点
1.不会讲线段

2.考虑不到利用椭圆的定义求解
知识点
11.如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
正确答案
解析
将该几何体的三视图放到正方体中考虑,得到该几何体为四棱锥S-ABCD,其中底面为长方形,长为

















考查方向
本题主要考查由三视图还原直观图、球的切接等知识,意在考查考生空间想象能力、运算求解能力等,对考生的要求很高。
解题思路
1.先根据题中给出的三视图确定该几何体的直观图为四棱锥;
2.确定四棱锥外接球的球心在的位置,然后建立方程组求出R即可。
易错点
1.无法根据三视图还原成原来的几何体;
2.无法确定外接球的球心所在位置,导致一点思路也没有。
知识点
6.已知定义在R上的函数





正确答案
解析
由






考查方向
本题主要考查函数的奇偶性、周期性、对数函数的运算等知识,意在考查考生对于抽象函数的理解能力和逻辑推理的能力。
解题思路
1.先根据条件判断出函数
2.利用周期函数将

易错点
1.不知道

2.不会化简
知识点
14.在Rt△ABC中,∠A=90°,AB=AC=2,点D为AC中点,点E满足

正确答案
-2
解析


所以
考查方向
本题主要考查向量的线性运算、平面向量基本定理以及向量的数量积等知识,意在考查考生的运算能力和逻辑推理能力。
解题思路
1.先将向量

2.利用数量积运算求出所求答案。
易错点
1.不会将所求的向量都用基底表示出来;
2.向量的数量积运算律和实数的运算混淆。
知识点
16.已知数列






正确答案
解析

当

由①-②得到, 
(1)当

化简得
所以当n为奇数时,
(2)当

即

带入得到
所以当n为偶数时
所以
当n为奇数时,

所以
即
当n为偶数时,

所以
即
综上得实数

考查方向
解题思路
1.先根据
2.对于递推公式分奇数、偶数讨论后求出通项公式,然后带入
易错点
1.对于

2.对于
知识点
13.已知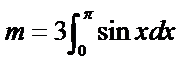
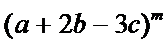
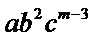
正确答案
-6480
解析
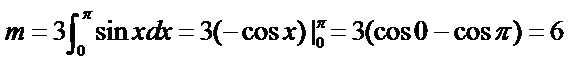
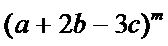
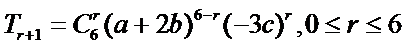
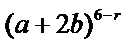
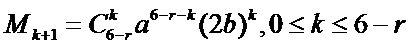
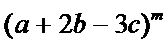
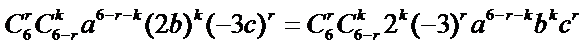
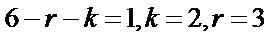
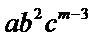
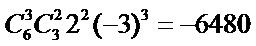
考查方向
解题思路
1.先利用定积分求出m的值;
2.写出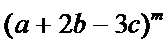
易错点
1. 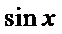
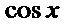
2.对于三项的二项式定理不知道怎么办。
知识点
15.已知双曲线


正确答案
解析
双曲线










考查方向
本题主要考查双曲线的渐近线方程,直线与圆的位置关系,点到直线的距离公式等知识,意在考查考生运算求解能力和转化与化归的能力。
解题思路
1.先求出圆心到双曲线渐近线的距离;
2.利用点到直线的距离公式表示出
易错点
1.渐近线的方程求错;
2.不会数形结合由弦长转化为求点到直线的距离。