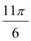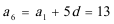- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知角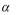
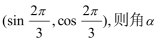
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.不等式组
正确答案
36
解析
解析已在路上飞奔,马上就到!
知识点
9.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.不共面的四个定点到平面

正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
12.已知周期函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.复数
正确答案
(-1)
解析
解析已在路上飞奔,马上就到!
知识点
7.在等差数列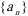
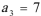

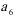
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.每次抛掷一枚骰子(六个面上分别标以1,2,3,4,5,6)。连续抛掷2次,则2次向上的数之和不小于10的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数
①
②
③
④
其中可能成立的个数为( )
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
5.已知向量a,b满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.为了在运行如下所示的伪代码后输出的y值为16,应输入的整数
正确答案
-5
解析
解析已在路上飞奔,马上就到!
知识点
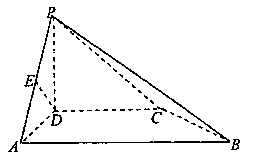
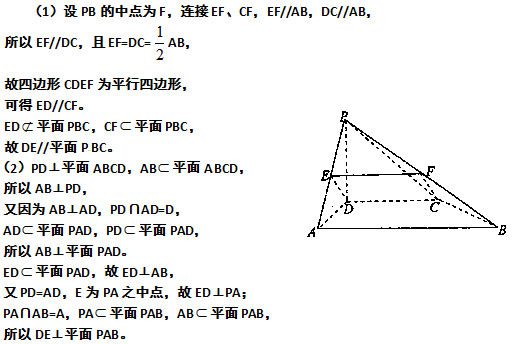
16.如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC//AB,∠BAD=90°,且AB=2AD=2DC=2PD=4(单位:cm),E为PA的中点。
(1)证明:DE//平面PBC;
(2)证明:DE⊥平面PAB;
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知
(1)若
(2)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修保养、费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额为y元。
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理有两种方案:
①当年平均盈利额达到最大值时,以30万元价格处理该机床;
②当盈利额达到最大值时,以12万元价格处理该机床。问哪种方案处理较为合理?请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知平面直角坐标系
(1)求圆C的方程;
(2)若过点(2,6)的直线l被圆C所截得的弦长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.将数列
记表中的第一列数





(I)证明数列

(II)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数。当
1

记表中的第一列数






(Ⅰ)证明数列

(Ⅱ)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当

正确答案
20.设函数
(1)当p=2时,求与函数
(2)若函数
(3)若在[1,e]上至少存在一点
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.[选做题]
在下面A,B,C,D四个小题中只能选做两题。
A.选修4-1:几何证明选讲
如图,


B.选修4-2:矩阵与变换
已知矩阵
C.选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是
D.选修4-5:不等式选讲
已知

正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
22.利用空间向量的方法解决下列问题:在正方形

(1)求AE与
(2)证明AE⊥面
22.利用空
(1)求AE与D1F所成的角;
(2)证明AE⊥面A1D1F。
正确答案
23.如图,若M是抛物线
正确答案
解析
解析已在路上飞奔,马上就到!