- 真题试卷
- 模拟试卷
- 预测试卷
在右图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2, 记∠ABC=θ。
17.求用含θ的代数式表示DC;
18.求△BCD面积S的最小值.
正确答案
解析
试题分析:本题属于解三角形,题难道不大,关键是找对在哪个三角形中解决问题,另外此题巧妙的与三角形求最值结合了起来。
在△ADC中,∠ADC=360°-90°-120°-θ=150°-θ,
由正弦定理可得
即
于是
考查方向
本题考查的是:1,利用正弦定理接三角形;
2,结合三角函数求最值,求三角形面积的最值.
解题思路
解题步骤如下:1、先求∠ADC,再在三角形ACD中借助正弦定理求DC,
2、利用(I)的结论,然后在三角形ABC中有正弦定理求BC,利用三角形面积公式求面积,最后结合三角函数求最值的方法求面积的最值。
易错点
1、不知在哪个三角形中求DC;
2、不会借助三角函数求三角形的面积的最值。
正确答案
θ=75°时,S取得最小值
解析
试题分析:本题属于解三角形,题难道不大,关键是找对在哪个三角形中解决问题,另外此题巧妙的与三角形求最值结合了起来。
在△ABC中,由正弦定理得
即
由(Ⅰ)知:
那么
故θ=75°时,S取得最小值
考查方向
本题考查的是:1,利用正弦定理接三角形;
2,结合三角函数求最值,求三角形面积的最值.
解题思路
解题步骤如下:1、先求∠ADC,再在三角形ACD中借助正弦定理求DC,
2、利用(I)的结论,然后在三角形ABC中有正弦定理求BC,利用三角形面积公式求面积,最后结合三角函数求最值的方法求面积的最值。
易错点
1、不知在哪个三角形中求DC;
2、不会借助三角函数求三角形的面积的最值。
某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
22.若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
23.若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
正确答案
解析
试题分析:本题属于高考中涉及到概率的常见题型,只是分类时要清楚,以免出错。记顾客获得半价优惠为事件A,则
两个顾客至少一个人获得半价优惠的概率
考查方向
解题思路
本题第一问先求顾客获得半价优惠的概率,然后再利用对立事件去求两个顾客至少一个人获得半价优惠的概率;第二问先求方案二中付款金额的分布列,然后再求方差,这样再与方案一的付款金额做比较,就可得出结论。
易错点
1、第一问若用分类讨论的话,可能会讨论不清,不会用对立事件来解题。
2、第二问会在计算X=224、X=256的概率时出错,因为取到两个红球和一个红球分别会出现三种情况。
正确答案
第二种方案比较划算.
解析
试题分析:本题属于高考中涉及到概率的常见题型,只是分类时要清楚,以免出错。
若选择方案一,则付款金额为320-50=270元.
若选择方案二,记付款金额为X元,则X可取160,224,256,320.
∵ 270>240,
∴第二种方案比较划算.
考查方向
解题思路
本题第一问先求顾客获得半价优惠的概率,然后再利用对立事件去求两个顾客至少一个人获得半价优惠的概率;第二问先求方案二中付款金额的分布列,然后再求方差,这样再与方案一的付款金额做比较,就可得出结论。
易错点
1、第一问若用分类讨论的话,可能会讨论不清,不会用对立事件来解题。
2、第二问会在计算X=224、X=256的概率时出错,因为取到两个红球和一个红球分别会出现三种情况。
已知函数f(x)=2x- 
26.求f(x)的最大值;
27.己知x∈(0,1),
正确答案
f(x)取得最大值2ln2-1
解析
试题分析:本题属于导数应用中的常规问题,题目的难度是逐渐由易到难,所以应重点分析a的不同情况。f(x)=2-ex,

所以f(x)在(-∞,ln2)上单调递增,
在(ln2,+∞)上单调递减,
则当x=ln2时,
f(x)取得最大值2ln2-1.
考查方向
解题思路
本题考查导数的性质,解题步骤如下:1、求导,然后解导数不等式,从而的函数的单调区间,进而求得函数的最大值。
2、对参数分类讨论研究不等式恒成立,因为f(x)在(0,1)上大于0,故先从 a≤0与a>0两个角度去讨论,而当a>0时,因所构造的函数在已知区间上的单调性不同,故又分0<a≤1和a>1两种情况。
易错点
参数的讨论是易错点
正确答案
a的取值范围是a≤1.
解析
试题分析:本题属于导数应用中的常规问题,题目的难度是逐渐由易到难,所以应重点分析a的不同情况。
x∈(0,1)时,f(x)在(0,ln2)上单调递增,在(ln2,1)上单调递减,
且f(0)=0,f(1)=3-e>0,所以此时f(x)>0,
因为tanx>0,所以当a≤0时,af(x)≤0<tanx.
当a>0时,令g(x)=tanx-af(x),
则
故
(ⅰ)当0<a≤1时,

所以g(x)在(0,1)上单调递增,
又g(0)=0,
所以此时g(x)>0,
即af(x)<tanx成立;
(ⅱ)当a>1时,
所以存在x0∈(0,1)使得
即x∈(0,x0)时,g(x)<0,g(x)单调递减,
又g(0)=0,
所以此时g(x)<0,
与af(x)<tanx矛盾;
综上,a的取值范围是a≤1.
考查方向
解题思路
本题考查导数的性质,解题步骤如下:1、求导,然后解导数不等式,从而的函数的单调区间,进而求得函数的最大值。
2、对参数分类讨论研究不等式恒成立,因为f(x)在(0,1)上大于0,故先从 a≤0与a>0两个角度去讨论,而当a>0时,因所构造的函数在已知区间上的单调性不同,故又分0<a≤1和a>1两种情况。
易错点
参数的讨论是易错点
如图,AB与圆O相切于点B,CD为圆O上两点,延长AD交圆O于点E,BF∥CD且交ED于点F
28.证明:△BCE∽△FDB;
29.若BE为圆O的直径,∠EBF=∠CBD,BF=2,求AD·ED.
正确答案
证明略
解析
试题分析: 本题是几何证明中的基本题型,整个题目的难度不大。属简单题目。因为BF∥CD,所以∠EDC=∠BFD,
又∠EBC=∠EDC,
所以∠EBC=∠BFD,
又∠BCE=∠BDF,
所以△BCE∽△FDB.
考查方向
解题思路
1、证△BCE∽△FDB;
2、通过求BD,借助三角形ABE为直角三角形,利用射影定理即可求得。
易错点
第二问不能从三角形相似的角度去研究所求问题。
正确答案
AD·ED=2
解析
试题分析: 本题是几何证明中的基本题型,整个题目的难度不大。属简单题目。
因为∠EBF=∠CBD,所以∠EBC=∠FBD,
由(Ⅰ)得∠EBC=∠BFD,所以∠FBD=∠BFD,
又因为BE为圆O的直径,
所以△FDB为等腰直角三角形,BD=

因为AB与圆O相切于点B,所以EB⊥AB,即AD·ED=BD2=2
考查方向
解题思路
1、证△BCE∽△FDB;
2、通过求BD,借助三角形ABE为直角三角形,利用射影定理即可求得。
易错点
第二问不能从三角形相似的角度去研究所求问题。
如图,直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=号,M为BB1的中点,Ol为上底面对角线的交点.
20.求证:O1M⊥平面ACM;
21.求AD1与平面ADM所成角的正弦值.
正确答案
证明略
解析
试题分析:本题属于立体几何中的常见题型.利用线面垂直的判定定理,证垂直;利用空间向量求角。连接AO1,BD
在直四棱柱ABCD-A1B1C1D1中,BB1⊥平面ABCD,AC平面ABCD,所以BB1⊥AC,
∵ 四边形ABCD是边长为2的菱形,
∴ AC⊥BD,
又∵ BD∩BB1=B,
∴ AC⊥平面DBB1D1,
又∵ O1M平面DBB1D1,
∴ AC⊥O1M.
∵ 直四棱柱所有棱长均为2,
∠BAD=,M为BB1的中点,
∴ BD=2,AC=2,B1M=BM=1,
∴ O1M2=O1B12+B1M2=2,AM2=AB2+BM 2=5,O1A2=O1A12+A1A2=7,
∴ O1M2+AM2=O1A2,∴ O1M⊥AM.
又∵ AC∩AM=A,∴ O1M⊥平面ACM.
考查方向
本题主要考察了1、线面垂直,
2、利用空间向量求直线与平面所成角.
解题思路
本题考查立体几何,解题步骤如下:1、在证明O1M⊥平面ACM时,利用线面垂直的判定定理,先证AC⊥平面DBB1D1,从而得AC⊥O1M,然后再在三角形AM O1中利用勾股定理去证明O1M⊥AM ,从而得证。
2、先建空间坐标系,然后再去求向量AD1与平面ADM的法向量,当求得这两个向量夹角的余弦值时,就可AD1与平面ADM所成角的正弦值
易错点
1、第一问中O1M⊥AM可能想不到利用直角三角形的勾股定理去证明。
2、第二问用空间向量解题可能会出现运算错误。
正确答案
AD1与平面ADM所成角的正弦值为.
解析
试题分析:本题属于立体几何中的常见题型.利用线面垂直的判定定理,证垂直;利用空间向量求角。设BD交AC于点O,连接OO1,
以O为坐标原点,OA,OB,OO1所在直线分别为x轴,y轴,z轴建立空间直角坐标系O-xyz,则A(,0,0),D(0,-1,0),D1(0,-1,2),M(0,1,1),
设平面ADM的一个法向量n=(x,y,z),
则
令x=1,得
设AD1与平面ADM所成角为
则
即AD1与平面ADM所成角的正弦值为
考查方向
本题主要考察了1、线面垂直,
2、利用空间向量求直线与平面所成角.
解题思路
本题考查立体几何,解题步骤如下:1、在证明O1M⊥平面ACM时,利用线面垂直的判定定理,先证AC⊥平面DBB1D1,从而得AC⊥O1M,然后再在三角形AM O1中利用勾股定理去证明O1M⊥AM ,从而得证。
2、先建空间坐标系,然后再去求向量AD1与平面ADM的法向量,当求得这两个向量夹角的余弦值时,就可AD1与平面ADM所成角的正弦值
易错点
1、第一问中O1M⊥AM可能想不到利用直角三角形的勾股定理去证明。
2、第二问用空间向量解题可能会出现运算错误。
在△ABC中,A(-l,0),B(1,0),若△ABC的重心G和垂心H满足GH平行于x轴( G,H不重合).
24.求动点C的轨迹
25.己知O为坐标原点,若直线AC与以O为圆心,以|OH|为半径的圆相切,求此时直线AC的方程.
正确答案
解析
试题分析:本题属于解析几何中的基本问题,题目的难度不大,但是题目设计的是环环相扣,点与点的关系处理不当,就会事倍功半。
由题意可设C (x,y),则
因为H为垂心,所以
整理可得
即动点C的轨迹Г的方程为
考查方向
本题考查了解析几何中的求轨迹问题、直线与圆的位置关系。
解题思路
解题步骤如下:1、设点C (x,y),利用C、G、H的关系确定其坐标,
2、通过BH与AC垂直,构造向量垂直,利用数量积为0,得到所求轨迹方程,要去掉不合题意的点。
3、 通过直线AC与轨迹
易错点
1、第一问不能利用G、H两点的关系表达两点的坐标,再就是没把不符合条件的点去掉;
2、第二问不会利用直线与曲线
正确答案
y=x+1或y=-x-1.
解析
试题分析:本题属于解析几何中的基本问题,题目的难度不大,但是题目设计的是环环相扣,点与点的关系处理不当,就会事倍功半。
显然直线AC的斜率存在,设AC方程为y=k(x+1),C(x0,y0).
将y=k(x+1)代入
解得

原点O到直线AC的距离
依题意可得
即
故所求直线AC的方程为y=x+1或y=-x-1.
考查方向
本题考查了解析几何中的求轨迹问题、直线与圆的位置关系。
解题思路
解题步骤如下:1、设点C (x,y),利用C、G、H的关系确定其坐标,
2、通过BH与AC垂直,构造向量垂直,利用数量积为0,得到所求轨迹方程,要去掉不合题意的点。
3、 通过直线AC与轨迹
易错点
1、第一问不能利用G、H两点的关系表达两点的坐标,再就是没把不符合条件的点去掉;
2、第二问不会利用直线与曲线
2.复数
正确答案
解析


考查方向
解题思路
根据复数除法的运算法则,将其转化为
易错点
(1)复数的除法运算掌握不熟练,不能正确的转换为其代数形式,
(2)分不清实部与虚部。
知识点
4.(x-2y)6的展开式中,x4y2的系数为
正确答案
解析
由

考查方向
解题思路
利用二项展开式的通项公式
易错点
公式掌握不好,或运算失误;混淆系数与二项式系数。
知识点
10.某几何体的三视图如右图所示,则其体积为
正确答案
解析
由三视图可知该组合体是底面半径为1,高为8的圆柱从中间按45度斜切成两部分,然后其中一部分旋转90度,组成的几何体,因此组合体的体积与原圆柱的体积相等,为
考查方向
解题思路
由三视图可知该组合体是一个长为8的圆柱从中间按45度斜切成两部分,然后再由这两部分组合成的几何体。
易错点
不能正确还原几何体,看不出该组合体是两个圆柱的组合体。
1.设A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A
正确答案
解析
因为A是B的子集,所以B中必有元素1,2.而集合{3,4}的子集个数为
考查方向
解题思路
因为A是B的子集,所以B中必有元素1,2.因此集合B的个数实际上就转换为集合{3,4}的子集个数。
易错点
子集个数问题,此题比较简单,也可一一列举,但注意列举时要有规律。
知识点
9.己知A(x1,0),B(x2,1)在函数f(x)=2sin(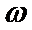
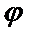
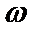
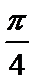
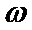
正确答案
解析
将点A,B代入f(x)表达式,得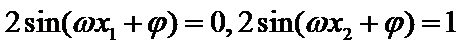
解得: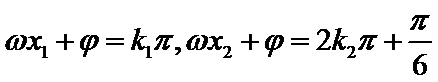
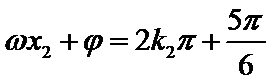
两式相减得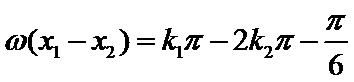
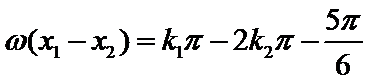
因此当|x1-x2|的最小值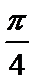
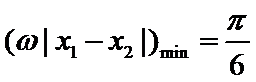
所以
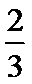
考查方向
解题思路
把点A,B代入函数表达式,然后求出|x1-x2|的关系式,然后研究其最小值即可。
易错点
不能正确理解题意。
知识点
5. A(
正确答案
解析
将A(

考查方向
解题思路
线将A点坐标代入抛物线x2=2py(p>0),求得p值,再结合点到焦点的距离公式求得。
易错点
由抛物线的标准方程没搞清焦点位置,以至于点到焦点的距离公式用错。
知识点
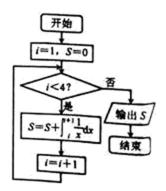
6.执行右侧的程序框图,输出S的值为
正确答案
解析
因为i<4,所以S=(ln2-ln1)+(ln3-ln2)+(ln4-ln3)=ln4,故选A。
考查方向
解题思路
先明确S=S+(ln(i+1)-lni),进而确定这是裂项相消求和。
易错点
1、对程序中的求和没理解到位;
2、能错结束程序的i值。
知识点
7.若x,y满足不等式组

正确答案
解析
画出线性区域,区域是三角形ABC内部包括边界,其中A(1,2),B(3,2)C(2,3),设原点为O,所以OA的斜率最大为2,故选A。
考查方向
解题思路
先画出线性区域,然后再求区域内的点与原点连线的斜率的最大值。
易错点
目标函数没能转化为斜率。
知识点
8.Sn为等比数列{an}的前n项和,满足al=l,
正确答案
解析
因为





考查方向
解题思路
因为




易错点
不能正确排除干扰选项-3和-2。
知识点
3.已知向量a,b满足a·(a-b)=2,且|a|=1,|b|=2,则a与b的夹角为
正确答案
解析
由



考查方向
解题思路
由已知先求

易错点
向量的夹角的余弦公式不清楚。
知识点
12.数列{an}的通项公式为an =
①{an}为先减后增数列;
②{an}为递减数列:
③
④
其中正确命题的序号为
正确答案
解析
先取对数得
由此可知an的单调性与
故此先研究
构造函数

所以
由此可知

又因
所以
因此函数
故{an}为递减数列,
且
故选C。
考查方向
本题主要考查了数列的单调性与有界性
解题思路
首先取对数得



易错点
对于数列单调性无从下手。
知识点
11.F为双曲线


正确答案
解析
若设双曲线的左焦点为F’,
连接P F’,
由几何关系可知三角形P F’F是直角三角形,
PF’=
所以PF’-PF=
所以e=
故选D。
考查方向
解题思路
若设双曲线的左焦点为F’, 连接P F’,由几何关系可知三角形P F’F是直角三角形,然后利用双曲线的定义即的a与c的关系,从而求得离心率。
易错点
若设双曲线的左焦点为F’,不能想到连接P F’,利用双曲线的定义解题。
知识点
13.在等差数列{an}中,a4=-2,且al+a2+...+a10=65,则公差d的值是 。
正确答案
3
解析
先用性质解题:al+a2+...+a10=5(a4+ a7)=65,
所以(a4+ a7)= 13,
因此a7=11,
考查方向
解题思路
一是用基本量解题,列方程组;二是结合性质解题。
易错点
若用基本量表示前10项的和与a4,则运算要细心,否则就结合性质解题。
知识点
15.已知f(x)为奇函数,函数g(x)与f(x)的图象关于直线y=x+l对称,若g(1)=4,则f(一3)=____.
正确答案
-2
解析
因为g(1)=4,所以点(1,4)在函数g(x)的图像上,设(1,4)关于直线y=x+l的对称点为(m,n),所以有
考查方向
解题思路
先求出点(1,4)关于直线y=x+l的对称点(3,2),所以有f(3)=2,再利用奇函数的性质可求得f(-3)。
易错点
不能求出(1,4)关于直线y=x+l的对称点。
知识点
14.1000名考生的某次成绩近似服从正态分布N(530, 502),则成绩在630分以上的考生人数约为____.(注:正态总体

正确答案
23
解析


考查方向
解题思路
利用注解中的公式可求得成绩在630分以上的概率,然后再求人数。
易错点
可能会出现用错公式的现象。
知识点
16.一个几何体由八个面围成,每个面都是正三角形,有四个顶点在同一平面内且为正方形,从该几何体的12条棱所在直线中任取2条,所成角为60°的直线共有 对.
正确答案
48
解析
该几何体是两个全等的正四棱锥底面重合,对接成的组合体,其中侧面均为正三角形。先从相交直线入手,成60°的直线有24对,在考虑异面直线,成60°的直线有24对也有24对,所以共计48对
考查方向
解题思路
分两种类,一类是求所成角为60°的相交直线的对数,另一类是求所成角为60°的异面直线的对数。
易错点
一是几何体的结构想象不出来,还有就是所成角为60°的直线有相交直线,也有异面直线,异面直线可能会出现重复或遗漏。