- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.实数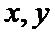
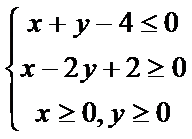
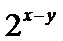
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.阅读程序框图,若输入m=4,n=6,则输出
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 设三位数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下列说法中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.
正确答案
- 5
解析
解析已在路上飞奔,马上就到!
知识点
13. 在数列


正确答案
- 1
解析
解析已在路上飞奔,马上就到!
知识点
14.已知二次函数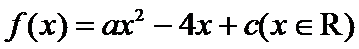
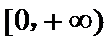
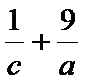
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量



正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知












①
②
③
④
则在区间

正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
20.已知
(Ⅰ)当

(Ⅱ)当


(Ⅲ)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设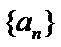
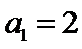
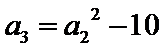
(Ⅰ)求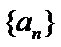
(Ⅱ)设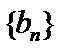
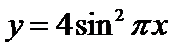
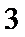
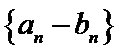
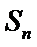
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
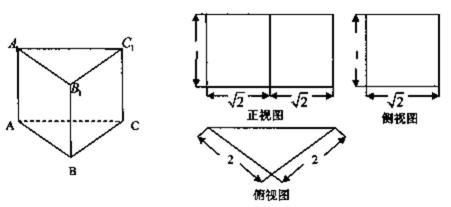
19.已知直三棱柱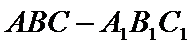

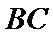
(Ⅰ)求证: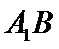
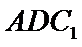
(Ⅱ)求二面角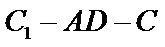
(Ⅲ)试问线段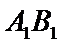
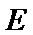
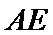
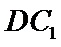
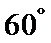
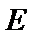
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)


(Ⅱ)若


(Ⅲ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知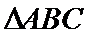
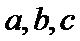
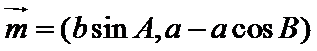
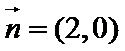
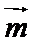
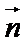
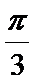
(Ⅰ)求角B的大小;
(Ⅱ)求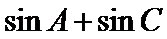
正确答案
解析
解析已在路上飞奔,马上就到!