• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
  • 教师招募
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
理科数学 安阳市2013年高三试卷
精品
|
立即下载

理科数学 热门试卷

X 查看更多试卷
试卷目录
1、单选题
1
2
3
4
5
6
7
8
9
10
11
12
2、填空题
13
14
15
16
3、简答题
17
18
19
20
21
22
  • 真题试卷
  • 模拟试卷
  • 预测试卷
查看更多 >
单选题 本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。
1
题型： 单选题
|
分值: 5分

9.直线到点和的距离分别是和，则符合条件的直线的条数是（   ）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率
1
题型： 单选题
|
分值: 5分

1.若是虚数单位，则复数－等于（     ）

A0

B2

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的混合运算
1
题型： 单选题
|
分值: 5分

3.设分别是椭圆的左、右焦点，过的直线相交于两点，且成等差数列，则的长为（   ）

A

B1

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程
1
题型： 单选题
|
分值: 5分

6.同时具有性质“①最小正周期是，②图象关于直线对称；③在上是增函数”的一个函数是：（   ）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型： 单选题
|
分值: 5分

8.若，则（   ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项
1
题型： 单选题
|
分值: 5分

11.设等差数列的前n项和为，若，则中最大的是（   ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项
1
题型： 单选题
|
分值: 5分

4.已知某几何体的三视图如图所示，则该几何体的体积为（   ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图
1
题型： 单选题
|
分值: 5分

7.函数是奇函数，则（   ）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型： 单选题
|
分值: 5分

10.已知点在曲线上，为曲线在点处的切线的倾斜角，则的取值范围是（   ）

A[0,)

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程
1
题型： 单选题
|
分值: 5分

12.函数的图像大致为（   ）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化
1
题型： 单选题
|
分值: 5分

5.对一位运动员的心脏跳动检测了8次，得到如下表所示的数据：

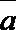
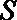
上述数据的统计分析中，一部分计算见程序框图（其中是这8个数据的平均数），则输出的的值是（   ）

A6

B7

C8

D56

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

极差、方差与标准差循环结构
1
题型： 单选题
|
分值: 5分

2.设为等比数列的前项和，，则（   ）

A5

B11

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项
填空题 本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。
1
题型：填空题
|
分值: 5分

13.若函数的值域是则______.

正确答案

1

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域
1
题型：填空题
|
分值: 5分

15.设的内角A,B,C所对的边分别为,若,，则的取值范围为_____.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念
1
题型：填空题
|
分值: 5分

16.设是双曲线的右焦点，直线交双曲左右两支于，若，则双曲线的离心率等于_____。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程
1
题型：填空题
|
分值: 5分

14.若任取，则点满足的概率为______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系
简答题（综合题） 本大题共70分。简答应写出文字说明、证明过程或演算步骤。
1
题型：简答题
|
分值: 12分

19.已知四棱锥底面ABCD是矩形，PA⊥平面ABCD， AD＝2，AB＝1，E．F分别是线段AB．BC的中点，

（I）证明：PF⊥FD；

（II）在线段 PA上找一点G，使得EG∥平面PFD；

（III）若与平面所成的角为，求二面角的余弦值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征
1
题型：简答题
|
分值: 12分

20.设函数

（1）的最小值；

（2）数的单调性；

（3）直线与曲线交于两点，求证：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型：简答题
|
分值: 12分

21.已知抛物线在x轴的正半轴上，过M的直线与C相交于A、B两点，O为坐标原点。

（I）若m=1，且直线的斜率为1，求以AB为直径的圆的方程；

（II）问是否存在定点M，不论直线绕点M如何转动，使得恒为定值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用
1
题型：简答题
|
分值: 10分

请22、23两题中选一题作答

22.选修4—1：几何证明选讲

如图，⊙O的半径OB垂直于直径AC，M为AO上一点，BM的延长线交⊙O于N,过N点的切线交CA的延长线于P。

（1）求证：PM2=PA·PC

（2）若⊙O的半径为，OA=OM求：MN的长。

23.选修4－5：不等式选讲

设关于的不等式.

（I） 当，解上述不等式。

（II）若上述关于的不等式有解，求实数的取值范围。

正确答案

22.

23.

解析

解析已在路上飞奔，马上就到！

知识点

不等式
1
题型：简答题
|
分值: 12分

17.阅读下面材料：   根据两角和与差的正弦公式，有

------①

------②

由①+② 得------③

令 有

代入③得 .

（Ⅰ） 类比上述推理方法，根据两角和与差的余弦公式，证明:;

（Ⅱ）求值：(提示:如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念
1
题型：简答题
|
分值: 12分

18.甲、乙两人同时参加奥运志愿者的选拔赛，已知在备选的10道题中，甲能答对其中的6题，乙能答对其中的8题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才能入选．

（1）求甲答对试题数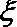的分布列及数学期望；

（2）求甲、乙两人至少有一人入选的概率．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

点击 “立即下载”

即可下载本试卷，含解析哦

知道啦