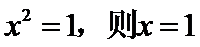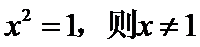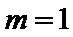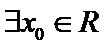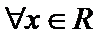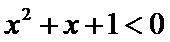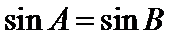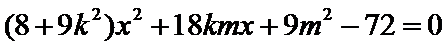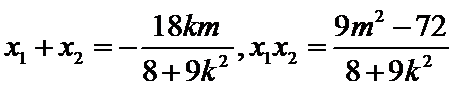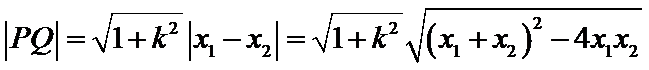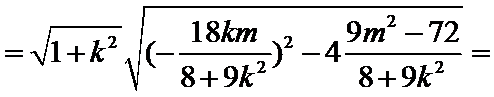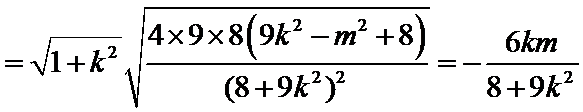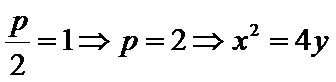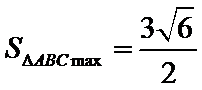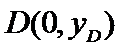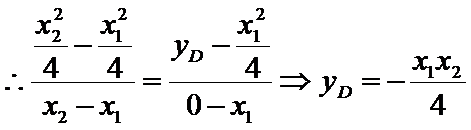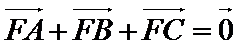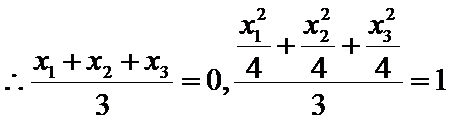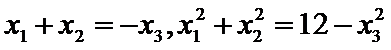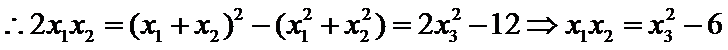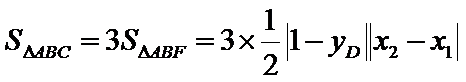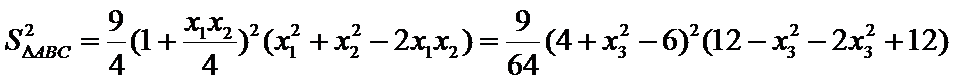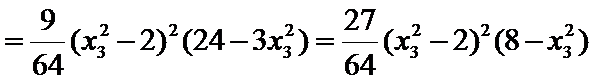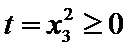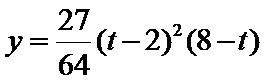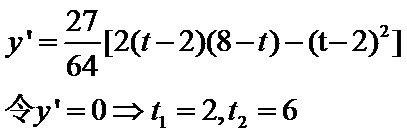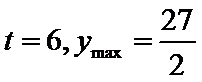- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合

正确答案
解析
因为










考查方向
解题思路
1)解不等式

2)求
易错点
本题易在求集合A的时出现错误,易忽视二元一次不等式中二次项系数应先变为正数,再解不等式;以及只是不等式在解时注意单调性.
知识点
2.已知




正确答案
解析
因为

考查方向
解题思路
1)先化简解
2)求
易错点
本题容易求出

知识点
3.下列有关命题的说法正确的是
正确答案
解析
命题“若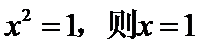
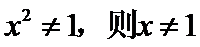

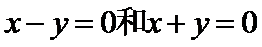
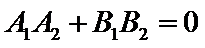
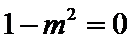

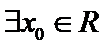
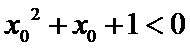
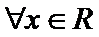
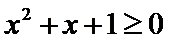
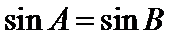
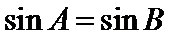
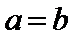
考查方向
解题思路
1)否命题的定义是否定题设和结论;
2)两直线垂直的充要条件是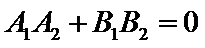
3)特称命题的否定是将特称改为全称,否定结论;
4)逆命题是题设和结论互换,然后判断若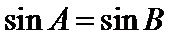
易错点
本题易在判定命题的否定和否命题时出现错误,以及判断必要条件时出现错误,两直线垂直的充要条件用错,三角形中角和正弦值之间的关系也易错。
知识点
4.要得到函数

正确答案
解析
由诱导公式可得




考查方向
解题思路
1)先将

2)先平移再伸缩。
易错点
本题容易忘记变换三角函数名称,
知识点
6.各大学在高考录取时采取专业志愿优先的录取原则.一考生从某大学所给的7个专业中,选择3个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生填报专业志愿的方法有 种。
正确答案
解析
第一类,选甲乙中的一个,除了甲乙,还有5个专业可选,所以有


考查方向
解题思路
1)把甲乙看成一组,剩下的5个专业看成一组;
2)从两组中分别选专业,共选3个;
3)将选好的专业进行排列;
易错点
本题易把甲乙两种专业和其他五个专业混到一起选出现错误看成一个整体时出现错误,易出现“
知识点
8.若


正确答案
解析
将









考查方向
解题思路
1)作出


2) 由图象判定最优解与最优点;
3) 再加绝对值.
易错点
本题易在求目标函数的最值时出现问题,忘记加对值。
知识点
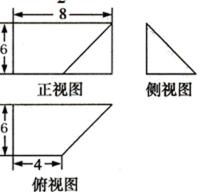
5.一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是
正确答案
解析
由三视图,可知该几何体的直观图如图所示,取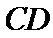
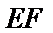
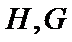
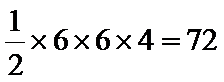
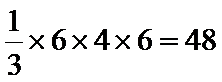
考查方向
解题思路
1)根据几何体的三视图,画出该几何体的直观图;
2) 分割几何体,分别判定几何体形状求其体积;
3)求和,即得该几何体的体积。
易错点
本题易在分割几何体时出现错误,而且求锥体的体积忘记乘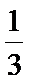
知识点
7.执行如图所示的程序框图,则输出的
正确答案
解析
当








考查方向
解题思路
1)先有框图计算出一些值,找到循环周期;
2)根据周期将条件

3)再按照化简后的条件重新循环,得到结果。
易错点
本题易在循环结构的终止时
知识点
9.设





正确答案
解析
以







那么
如果

如图(2),
则轨迹是双曲线.
∴点A的轨迹为圆或椭圆或抛物线或双曲线.所以选D项。
考查方向
解题思路
1)以


2)用平面
3)考虑面
易错点
本题以






知识点
10.已知定义域为R的偶函数

有





正确答案
解析

且

令

又



当

若

则
即

若

即
即

综上

由函数
得函数
设
作出函数

要使函数

则
当

则
当

则

由

由判别式
整理得


由

由判别式
整理得






考查方向
解题思路
1)由已知的单调性奇偶性,球的函数的解析式;
2)解方程得到关于
3)用判别式可得
易错点
本题易在求函数解析式时出现错误。
知识点
11.若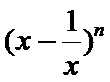
正确答案
-20
解析
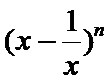
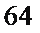
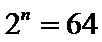
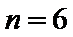
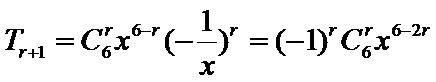
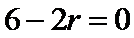
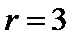
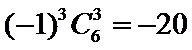
考查方向
解题思路
1)由所有项的二项式系数和为64可得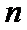
2)写出二项展开式的通项公式;
3)令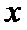
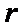
易错点
本题易把二项式系数和系数弄混。
知识点
12.已知函数
则
正确答案
-20
解析

所以

考查方向
解题思路
1) 把

2)代入第二段求值的通项公式;
易错点
本题易把

知识点
15.如图,B是AC的中点,











正确答案
②③④
解析
因为

















考查方向
解题思路
1)由已知条件



2)由平面向量基本定理得到
易错点
本题向量共线的充要条件,以及平面向量基本定理运用时容易出现错误。
知识点
13.海轮“和谐号”从A处以每小时21海里的速度出发,海轮“奋斗号”在A处北偏东

正确答案
解析
由题意做出平面图,如图所示,





考查方向
解题思路
1)根据题意,以及方向角,画出平面图形;
2)在
易错点
本题应当根据题意画出准确的图像,学生容易画错,计算也是 比较难的;
知识点
14.若点M是以椭圆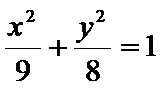
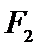
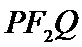
正确答案
解析
设直线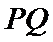
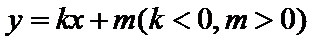
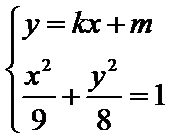
设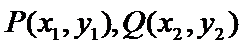
所以
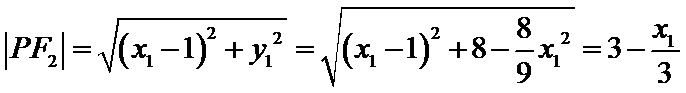
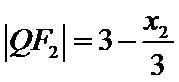
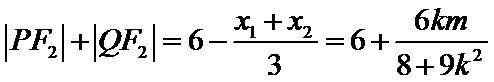
所以周长为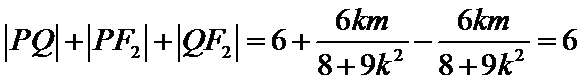
考查方向
解题思路
1)设出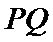
2)由弦长公式以及两点间距离公式求出边长,再求周长;
易错点
本题联立直线和椭圆的方程,容易在化简时出现错误;
知识点
已知等比数列



22.求数列

23.求数列

正确答案
(1)
解析
(1)设

故方程有两个不同的实根,由
从而

考查方向
解题思路
1)第一问设




2)第二问
易错点
错位相减法求和计算容易错。
正确答案
(2)
解析
(2)由(1)知
考查方向
解题思路
1)第一问设




2)第二问
易错点
错位相减法求和计算容易错。
在△ABC中,角A,B,C的对边分别为


16.求角A的大小;
17.设函数

正确答案
(1)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(1)在


在△ABC中,因为

所以


考查方向
解题思路
1)第一问中利用余弦定理得到

2)第二问中用倍角公式,和差公式可得
易错点
1)第一问中用余弦定理得到


2)第二问中用倍角公式,和差公式可得
正确答案
(2)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(2)由(1)得
令
即函数
考查方向
解题思路
1)第一问中利用余弦定理得到

2)第二问中用倍角公式,和差公式可得
易错点
1)第一问中用余弦定理得到


2)第二问中用倍角公式,和差公式可得
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出
《中华人民共和国环境保护法》规定食品的汞含量不得超过
18.检查人员从这



19.若从这批数量很大的鱼中任选




正确答案
(1)
考查方向
解题思路
1、第一问属于古典概型,直接用排列组合求出个数;
易错点
容易在排列组合问题计算时出现错误。
正确答案
(2)
解析
(2)依题意可知,这批罗非鱼中汞含量超标的鱼的概率





则


其分布列如下:
所以
考查方向
解题思路
1)第一问属于古典概型,直接用排列组合求出个数;
2)第二问中属于二项分布,各个事件之间是相互独立的,直接用公式求。
易错点
容易在排列组合问题计算时出现错误。
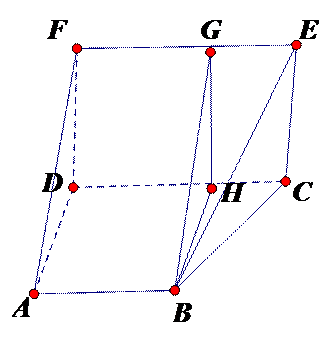
如图,多面体ABCDPE的底面ABCD是平行四边形,


20.若棱AP的中点为H,证明: HE∥平面ABCD
21.求二面角
正确答案
(1)略;
解析
(1)∵底面ABCD是平行四边形,

所以HE∥GC,HE

考查方向
解题思路
1)第一问通过平行四边形得到线线平行,由线面平行的判定定理得到线面平行;
2)第二问建立空间直角坐标系,求出两个面的法向量,再求出二面角的平面角。
易错点
直接找二面角,会出现找不到面的垂线的错误,若用空间向量,能得到两个面的向量的夹角,但是向量的夹角不一定是二面角的平面角。
正确答案
(2)
解析
(2)法一:如图,取PB的中点M,连接AC,DB交于点F,连接ME,MF,作FK⊥PB于点K,容易得到∠AKF是二面角A-PB-D的平面角




从而
由于点M是PB的中点,所以MF是△PDB的中位线,MF∥PD,且


故二面角
法二:由(1)知,DA,DC,DP两两互相垂直,建立空间直角坐标系
设平面PBE的法向量为








所以
从图形可知,二面角A-PB-E是钝角,所以二面角A-PB-E的大小为
考查方向
解题思路
1)第一问通过平行四边形得到线线平行,由线面平行的判定定理得到线面平行;
2)第二问建立空间直角坐标系,求出两个面的法向量,再求出二面角的平面角。
易错点
直接找二面角,会出现找不到面的垂线的错误,若用空间向量,能得到两个面的向量的夹角,但是向量的夹角不一定是二面角的平面角。
已知点F(0,1)为抛物线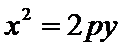
24.求抛物线C的方程;
25.点A、B、C是抛物线上三点且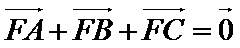
正确答案
(1)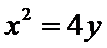
解析
(1)由题意知
考查方向
解题思路
1)第一问利用抛物线的定义,可求出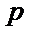
2)第二问首先设出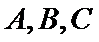
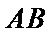
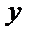
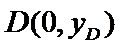
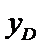
易错点
错位相减法求和计算容易错。
正确答案
(2)
解析
(2)令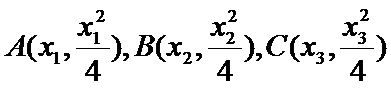
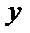
又因为
从而
令
当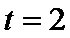
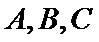
当
考查方向
解题思路
1)第一问利用抛物线的定义,可求出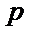
2)第二问首先设出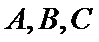
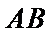
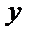
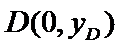
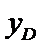
易错点
错位相减法求和计算容易错。
已知函数

26.若曲线



27.若



28.若


正确答案
(1)
解析
(1)当



考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
正确答案
(2)
解析
(2)由题意,

令
又
∴

∴
∴
∴
考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
正确答案
(3)综上,当





解析
(3)由

令


∴


∴
又令

令

∴


又
∴当

∴
同理,当



综上,当
当

当

考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,