- 真题试卷
- 模拟试卷
- 预测试卷
5.已知函数f(x)=则f(x)-f(-x)>-1的解集为( )
正确答案
解析
当0<x≤1时,-1≤-x<0,此时,f(x)=-x+1,f(-x)=-(-x)-1=x-1,
∴f(x)-f(-x)>-1化为-x+1-(x-1)>-1,解得x<
故所求不等式的解集为
方法二:画出函数f(x)=的图象如图所示.
由图可知f(x)为奇函数,从而由f(x)-f(-x)>-1,可知f(x)>
知识点
6.由曲线y=
正确答案
解析
知识点
7.已知函数f(x)=ax3+bsin x+4(a,b∈R),f(lg(log210))=5,则f(lg(lg 2))=( )
正确答案
解析
因为log

所以lg(log



知识点
1.已知a∈R,b∈R,若两集合相等,即
正确答案
解析
由已知得
知识点
2.下列命题中为真命题的是( )
正确答案
解析
对于A,当x=1时,x2+2x+1≠0,故A错;
对于B,当x0=1时,
对于C,当x=1时,log2x=0,故C错;
对于D,x+2x0+3=(x0+1)2+2≥2,故D错.
知识点
3.设


正确答案
解析
由已知





知识点
4.已知命题p:∃x∈R,x2-3x+3≤0,则下列说法正确的是 ( )
正确答案
解析
知识点
8.“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
正确答案
解析
当a=0时,f(x)=|(ax-1)x|=|x|在区间(0,+∞)上单调递增;
当a<0时,结合函数f(x)=|(ax-1)x|=|ax2-x|的图象知函数在(0,+∞)上单调递增,如图(1)所示:
当a>0时,结合函数f(x)=|(ax-1)x|=|ax
所以,要使函数f(x)=|(ax-1)x|在(0,+∞)上单调递增只需a≤0.
即“a≤0”是“函数f(x)=|(ax-1)x|在(0,+∞)上单调递增”的充要条件.
知识点
9.已知函数f(x)=若方程f(x)-a=0有三个不同的实数根,则实数a的取值范围为( )
正确答案
解析
画出函数f(x)的图象如图所示,
观察图象可知,若方程f(x)-a=0有三个不同的实数根,则函数y=f(x)的图象与直线y=a有3个不同的交点,此时需满足0<a<1,故选D.
知识点
10.设函数


正确答案
解析
知识点
11.若函数


正确答案
(0,2)
解析
知识点
15.设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),已知当x∈[0,1]时,f(x)=1-x,则:
①2是函数f(x)的周期;
②函数f(x)在(1,2)上递减,在(2,3)上递增;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=x-3.
其中所有正确命题的序号是( )
正确答案
①②④
解析
由已知条件:f(x+2)=f(x),
则y=f(x)是以2为周期的周期函数,①正确;当-1≤x≤0时0≤-x≤1,
f(x)=f(-x)=1+x,
函数y=f(x)的图像如图所示:
当3<x<4时,-1<x-4<0,
f(x)=f(x-4)=x-3,因此②④正确,③不正确.答案:①②④
知识点
12.若(a+1)

正确答案
解析
解析已在路上飞奔!
知识点
13.当x∈(1,2)时,不等式(x-1)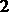
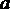
正确答案
{a|1<a≤2}
解析
设y=(x-1)2,y=logax.在同一坐标系中作出它们的图象,如图所示.
若0<a<1,则当x∈(1,2)时,(x-1)2<logax是不可能的,所以a应满足
解得1<a≤2.所以,a的取值范围为{a|1<a≤2}.
知识点
14.设






正确答案
解析
知识点
17.已知函数f(x)=ax+x2-xln a-b(a,b∈R,a>1),e是自然对数的底数.
(1)试判断函数f(x)在区间(0,+∞)上的单调性;
(2)当a=e ,b=4时,求整数k的值,使得函数f(x)在区间(k,k+1)上存在零点。
正确答案
解:(1)f′(x)=axln a+2x-ln a=2x+(ax-1)ln a.
∵a>1,∴当x∈(0,+∞)时,ln a>0,ax-1>0,
∴f′(x)>0,
∴函数f(x)在(0,+∞)上单调递增.
(2)∵f(x)=ex+x2-x-4,∴f′(x)=ex+2x-1,
∴f′(0)=0,
当x>0时,ex>1,∴f′(x)>0,
∴f(x)是(0,+∞)上的增函数;
同理,f(x)是(-∞,0)上的减函数.
又f(0)=-3<0,f(1)=e-4<0,f(2)=e2-2>0,
当x>2时,f(x)>0,
∴当x>0时,函数f(x)的零点在(1,2)内,
∴k=1满足条件;
f(0)=-3<0,f(-1)=-2<0,
f(-2)=+2>0,
当x<-2时,f(x)>0,
∴当x<0时,函数f(x)的零点在(-2,-1)内,
∴k=-2满足条件.
综上所述,k=1或-2.
解析
解析已在路上飞奔,马上就到!
知识点
18.函数f(x)=ln x-
(1)当a=-2时,求f(x)的最小值;
(2)若f(x)在[1,e]上的最小值为,求a的值。
正确答案
(1)当a=-2时,f(x)=
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
∴f(x)在(0,2)上为减函数,在(2,+∞)上为增函数.
∴f(x)min=f(2)=ln 2+1.
(2)f′(x)=
①当a≥-1时,对任意x∈[1,e],
f′(x)≥0,此时f(x)在[1,e]上为增函数,∴f(x)min=f(1)=-a=
∴a=
②当a≤-e时,对任意x∈[1,e],
f′(x)≤0,此时f(x)在[1,e]上为减函数.∴f(x)min=f(e)=1-

∴a=
③当-e<a<-1时,令f′(x)=0,得x=-a,当1<x<-a时,f′(x)<0,
f(x)在(1,-a)上递减.同理,f(x)在(-a,e)上递增.∴f(x)min=f(-a)=ln(-a)+1=
∴a=-

解析
解析已在路上飞奔,马上就到!
知识点
20.设函数f(x)=x2+bln(x+1),其中b≠0
(1)如果函数f(x)在定义域内既有极大值又有极小值,求实数b的取值范围;
(2)求证对任意的n∈N*不等式ln(

正确答案
(1)由题意f′(x)=2x+

即2x2+2x+b=0在(-1,+∞)有两个不等实根,
设g(x)=2x2+2x+b,则
△=4−8b>0且g(−1)>0,
0<b<
(2)对于函数f(x)=x2-ln(x+1),令函数h(x)=x3-f(x)=x3-x2+ln(x+1)
则h′(x)=3x2−2x+

当x∈[0,+∞)时,h'(x)>0,
所以函数h(x)在[0,+∞)上单调递增,
又h(0)=0,∴x∈(0,+∞)时,恒有h(x)>h(0)=0
即x2<x3+ln(x+1)恒成立.取x=
则有ln(

解析
解析已在路上飞奔,马上就到!
知识点
16.已知命题










正确答案
解:p真,任意

即

则a≤1
q真,则△=(a-1)2-4>0,即a>3或a<-1
∵“p或q”为真,“p且q”为假,∴p,q中必有一个为真,另一个为假
当p真q假时,有
当p假q真时,得a>3
∴实数a的取值范围为-1≤a≤1或a>3
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数f(x)=lg[
(1)分别求命题p、q为真命题时实数a的取值范围;
(2) 
正确答案
(1)命题



等价于
解得




命题




等价于
解得


(2)由(1)知,



而


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)求θ的值;
(2)若
(3)设



正确答案
(1)由题意,

即
∵θ∈(0,π),
∴


只须


结合θ∈(0,π),得
(2)由(1),得

∵
∴



即
而 

∴


即
而

综上,m的取值范围是
(3)构造

当



所以在[1,e]上不存在一个

当

因为


所以

故

F(x) min =F(1)= -2e<0,


解得
故
解析
解析已在路上飞奔,马上就到!