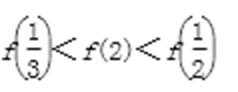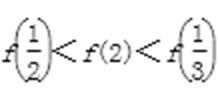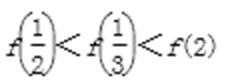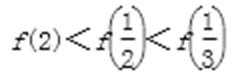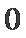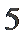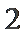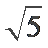- 真题试卷
- 模拟试卷
- 预测试卷
2、若
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9、已知数列
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10、设函数f（x）定义在实数集上，f（2－x）＝f（x），且当x≥1时，f（x）＝lnx，则有（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1、已知集合
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4、已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5、下列说法正确的是：（ ）
A命题“
B“x=－1”是“x2－5x－6=0”的必要不充分条件;
C命题“若x2=1，则x=1”的否命题是：若x2=1，则x≠1;
D命题“若x=y，则sin x=sin y”的逆否命题为真命题。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6、已知正项组成的等差数列{an}的前20项的和为100，那么a6·a15的最大值为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8、函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7、已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11、已知函数①y＝sin x＋cos x，②y＝2
A两个函数的图象均关于点
B两个函数的图象均关于直线x＝－
C两个函数在区间
D两个函数的最小正周期相同
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12、设f（x）、g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）·g（x）＋f（x）·g′（x）＞0，且g（－3）＝0，则不等式f（x）·g（x）＜0的解集是（ ）
正确答案
解析
记h（x）＝f（x）·g（x）．依题意得，h（－x）＝f（－x）·g（－x）＝－f（x）g（x），即h（－x）＝－h（x），所以函数h（x）是奇函数．当x＜0时，h′（x）＝f′（x）g（x）＋f（x）g′（x）＞0，h（x）是增函数，又h（－3）＝f（－3）·g（－3）＝0，因此，不等式h（x）＜0的解集是（－∞，－3）∪（0,3），即不等式f（x）·g（x）＜0的解集是（－∞，－3）∪（0,3），选D。
知识点
3、已知向量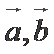
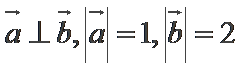
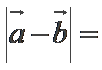
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14、由直线x＝－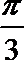
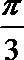
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15、函数
正确答案
解析
知识点
16．关于x的方程x3－3x2－a＝0有三个不同的实数解，则实数a的取值范围是________。
正确答案
（－4,0）
解析
由题意知使函数f（x）＝x3－3x2－a的极大值大于0且极小值小于0即可
又f′（x）＝3x2－6x＝3x（x－2）
令f′（x）＝0得，x1＝0，x2＝2
当x＜0时，f′（x）＞0；
当0＜x＜2时，f′（x）＜0；
当x＞2时，f′（x）＞0
所以当x＝0时，f（x）取得极大值，即f（x）极大值＝f（0）＝－a；
当x＝2时，f（x）取得极小值，即f（x）极小值＝f（2）＝－4－a
所以
知识点
13、已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21、已知函数f（x）＝xln x，
（1）求函数f（x）的极值点；
（2）设函数g（x）＝f（x）－a（x－1），其中a∈R，求函数g（x）在[1，e]上的最小值。（e＝2.718 28…）
正确答案
（2）g（x）＝xln x－a（x－1），则g′（x）＝ln x＋1－a.
g′（x）＜0⇔ln x＋1－a＜0⇔0＜x＜ea－1，
g′（x）＞0⇔x＞ea－1，
所以g（x）在（0，ea－1）上单调递减，在（ea－1，＋∞）上单调递增．
当ea－1≤1，即a≤1时，g（x）在[1，e]上单调递增，
所以g（x）在[1，e]上的最小值为g（1）＝0.
当1＜ea－1＜e，即1＜a＜2时，g（x）在[1，ea－1）上单调递减，
在（ea－1，e]上单调递增．
所以g（x）在[1，e]上的最小值为g（ea－1）＝a－ea－1.
当e≤ea－1，即a≥2时，g（x）在[1，e]上单调递减，
所以g（x）在[1，e]上的最小值为g（e）＝e＋a－ae.
综上，当a≤1时，g（x）的最小值为0；
当1＜a＜2时，g（x）的最小值为a－ea－1；
当a≥2时，g（x）的最小值为a＋e－ae。
解析
解析已在路上飞奔，马上就到！
知识点
20、已知函数
（1）求
（2）求
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．已知△ABC的内角A、B、C的对边分别为a、b、c， 
（1）求角C；
（2）若向量m＝（1，sin A）与n＝（2，sin B）共线，求a、b的值。
正确答案
解
解析
解析已在路上飞奔，马上就到！
知识点
18．已知数列{an}是等差数列，满足a2＝5，a4＝13.数列{bn}的前n项和是Tn，且Tn＋bn＝3。
（1）求数列{an}及数列{bn}的通项公式；
（2）若cn＝an·bn，试比较cn与cn＋1的大小。
正确答案
解
解析
解析已在路上飞奔，马上就到！
知识点
19．已知函数
（1）当a＝1时，求函数f（x）的图象在x＝3处的切线方程；
（2）若存在x＜0，使得f′（x）＝－9，求a的最大值。
正确答案
解 由已知，得f′（x）＝x2－（a＋1）x＋b.
由f′（0）＝0，得b＝0，f′（x）＝x（x－a－1）．
（1）当a＝1时，f（x）＝
所以函数f（x）的图象在x＝3处的切线方程为y－1＝3（x－3），即3x－y－8＝0.
（2）存在x＜0，使得f′（x）＝x（x－a－1）＝－9，
当且仅当x＝－3时，a＝－7.
所以a的最大值为－7。
解析
解析已在路上飞奔，马上就到！
知识点
22.
在下列三题中选一题作答。
1.如图，
若
（1）求证：
（2）求
2.已知直线
（1）若直线
（2）设曲线
3.已知正实数
（1）求
（2）设函数
正确答案
1.
2.
（1）曲线C的直角坐标方程为
即
直线l的方程为:
∵直线l与曲线C相切 ∴
即
（法二）①将
由
∵ 
（2）设
则 
∴ 
3.
（1）∵
又
∴ 
（2）
∴ 满足条件的实数
解析
解析已经在路上飞奔，马上就到。