- 真题试卷
- 模拟试卷
- 预测试卷
7.已知直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在复平面内,复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若

①若

②若

③若

④若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.将红、黑、白三个棋子放入如图所示的小方格内,每格内只放一个,且3个棋子既不同行也不同列,则不同的放法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若


①
②
③

④
其中正确命题的序号为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知映射




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在直三棱柱A1B1C1-ABC中,∠BAC=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出定义:若


①

②点
③函数
④函数
则其中真命题是__________。
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
13.在


正确答案
2048
解析
解析已在路上飞奔,马上就到!
知识点
18. 道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q<80时,为酒后驾车;当Q≥80时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有2人,依据上述材料回答下列问题:
(Ⅰ)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(Ⅱ)从违法驾车的8人中抽取2人,求取到醉酒驾车人数的分布列和期望。
(Ⅲ)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.1和0.25,且每位驾驶员是否发生交通事故是相互独立的。依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率(列式)。
正确答案
(Ⅰ)
(Ⅱ) 解:设取到醉酒驾车的人数为随机变量




则分布列如下

(Ⅲ)
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数
(1)若方程
(2)如果函数





正确答案
(1)由
求导数得到:




故


(2)

则
于是

要证:
只需证:
令



又




从而可知
从而原不等式得证.
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数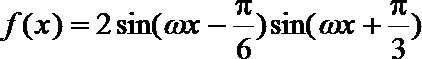
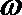
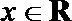

(1)求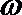
(2)在△
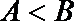
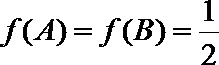
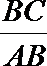
正确答案
(1)∵
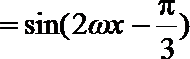
而
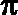
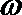
∴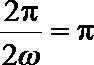
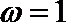
(2)由(1)得
若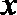
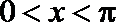
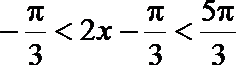
令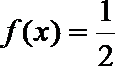
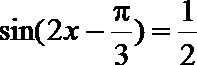

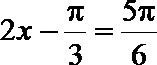
解之,得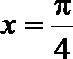
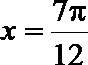
由已知,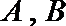

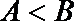
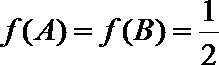
∴
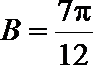
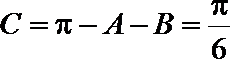
又由正弦定理,得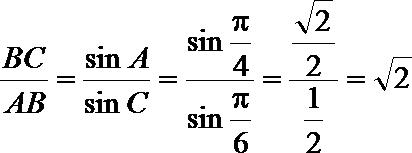
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱锥P-ABC中,



(1)求证:

(2)当


(3)当



正确答案
方法一:
(1)∵O、D分别为AC、PC中点,

(2)

又


(3)由(2)知,
∵D是PC的中点,
若点F是
∴直线OB在平面PBC内的射影为直线BD,

反之,当

∴O在平面PBC内的射影为
方法二:


以O为原点,射线OP为非负z轴,建立空间直角坐标系
设

设
(2)

又 
(3)

可求得平面PBC的法向量

设PA与平面PBC所成的角为

(3)



又


反之,当

∴O在平面PBC内的射影为
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知







(1)求动点

(2)过点









正确答案
(1)设


∵

∵


∴

∴
又

∴



(2)依题意,直线


设


则
消去

∴

∵

即




∴

∴
将①②代入上式可得
解析
解析已在路上飞奔,马上就到!
知识点
22. 数列


(1)数列
(2)求



正确答案
(1)数列
证明如下:
由




若存在



解得
于是

这与


(2)记




这时总存在




所以由









因此“存在



记


故

解析
解析已在路上飞奔,马上就到!











































































