理科数学朝阳区2014年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1.已知全集U={-1，0，1，2}，集合A={-1，2}，B={0，2}，则= （）

A{0}

B{2}

C{0，1，2}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交、并、补集的混合运算

题型：单选题

分值: 5分

8．对于函数与和区间E，如果存在，使，则我们称函数与在区间E上“互相接近”．那么下列所给的两个函数在区间上“互相接近”的是（）

A，

B，

C，

D，

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数恒成立问题导数的运算

题型：单选题

分值: 5分

4．已知条件，条件，则p是q的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既非充分也非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定

题型：单选题

分值: 5分

7．如图所示，正三角形中阴影部分的面积S是h(0≤h≤H)的函数，则该函数的图象是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

知图选式与知式选图函数图象的应用

题型：单选题

分值: 5分

2．函数的定义域（）

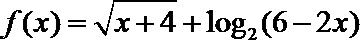
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法

题型：单选题

分值: 5分

3. 下列命题中正确的是（）

A若命题“且”是假命题，则“”也是假命题

B若命题“或”是真命题，则“q”是真命题

C原命题和否命题的真假一致

D命题“”的否定是“”

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

分值: 5分

5. 下列函数中，在内有零点且单调递增的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数零点的判断和求解

题型：单选题

分值: 5分

6.将函数图象上的所有点作关于轴对称,再向左平移个单位长度，所得曲线对应的函数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化对数函数的图像与性质

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

9. 已知函数，则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值导数的运算

题型：填空题

分值: 5分

10. 由曲线，，，所围成的封闭图形的面积为______ .（用数字作答）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用定积分求曲边梯形的面积

题型：填空题

分值: 5分

13．设，定义区间的长度为. 已知函数的定义域为，值域为，则区间的长度的最大值为_______，最小值的为_______.

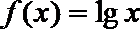
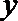
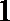
正确答案

2；1

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义

题型：填空题

分值: 5分

11.若，则的大小关系为___________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数值大小的比较不等式的性质

题型：填空题

分值: 5分

12．函数在上单调递增,则实数的取值范围是__________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的图象和性质

题型：填空题

分值: 5分

14. 设函数，给出下列4个命题：

①时，只有一个实数根；

②时，是奇函数；

③的图象关于点对称；

④方程至多有2个实数根，

上述命题中的所有正确命题的序号是_________.

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数性质的综合应用

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

19．已知函数

（1）当时，求函数的单调增区间；

（2）求的极大值；

（3）求证：对于任意，函数在上恒成立。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

16.已知函数.

（1）求曲线在点处的切线方程；

（2）求函数单调区间和极值.

（3）求函数在区间[0,2]上的最值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

17．已知函数

（1）求的值.

（2）画出函数的大致图象,并写出其单调区间.

（3）若关于x 的方程有两个不同的实根，求实数的取值范围.

正确答案

（1）

（2）单调增区间为，单调减区间为，

（3）

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数的值画函数的图象函数零点的判断和求解

题型：简答题

分值: 12分

15．已知集合， B=，,

（1）求；

（2）若，求的取值范围．

正确答案

（1）

（2）

解析

解析已在路上飞奔，马上就到！

知识点

交、并、补集的混合运算一元二次不等式的解法分式不等式的解法

题型：简答题

分值: 14分

18．解关于x的不等式

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

题型：简答题

分值: 14分

20.已知函数其中P,M是非空数集，且，设,.

（1）若，,求；

（2）是否存在实数，使得，且？若存在，请求出满足条件的实数;若不存在,请说明理由；

（3）若，且,,是单调递增函数，求集合P,M。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

子集与真子集交、并、补集的混合运算函数单调性的性质

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷