- 真题试卷
- 模拟试卷
- 预测试卷
9.点A、B、C、D均在同一球面上,其中



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设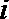
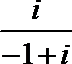
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如图所示,使电路接通,开关不同的开闭方式有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 若函数f(x)的图象如图所示,则f(x)的解析式可能是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数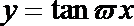
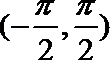
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若 △ABC 内接于以O为圆心,1为半径的圆,且

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知定点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图, 








(Ⅰ)求证:

(Ⅱ)求二面角
(Ⅲ)设点




正确答案
解析
解析已在路上飞奔,马上就到!
18.某市有A、B两所示范高中响应政府号召,对该市甲、乙两个教育落后地区开展支教活动.经上级研究决定:向甲地派出3名A校教师和2名B校教师,向乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
(Ⅰ)求互换后两校派往两地区教师人数不变的概率;
(Ⅱ)求互换后A校教师派往甲地人数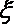
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.
(I)求
(II)求A的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(Ⅰ)当

(Ⅱ)讨论函数
(Ⅲ)设数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆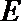
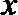
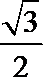
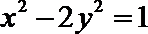
(Ⅰ)求椭圆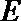
(Ⅱ)命题:“设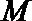
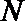
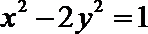
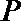
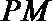
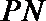

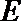
(Ⅲ)试推广(Ⅱ)中的命题,写出关于方程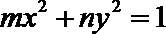
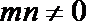

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请从22、23两题中选一题做答
22.选修4—1:几何证明选讲
如图








(1)求证:
(2)若
23.选修4-5:不等式选讲
已知


(Ⅰ)求
(Ⅱ)若


正确答案
22.
23.
解析
解析已在路上飞奔,马上就到!
知识点
14.已知实数


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在三棱锥

















正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.某同学为研究函数







正确答案
解析
解析已在路上飞奔,马上就到!