- 真题试卷
- 模拟试卷
- 预测试卷
1．已知集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．设集合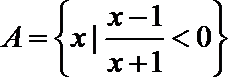
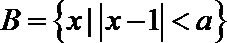
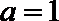
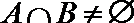
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知点
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．给出一个如图所示的程序框图，若要使输入的
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知一个空间几何体的三视图如图所示，根据图中标出的尺寸（单位：
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．不等式组
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．某工厂对一批产品进行了抽样检测.右图是根据抽样检 测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100)，[100，102)，[102，104),[104，106],已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ）．
正确答案
90
解析
解析已在路上飞奔，马上就到！
知识点
12．若各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（ ）．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知双曲线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．从集合｛A，B，C，D，E｝与｛1，3，5，7，9｝中各任取2个元素排成一排（字母和数字均不能重复），每排中字母A和数字9至多只出现一个的不同排法种数是（ ）．（用数字作答）。
正确答案
2016
解析
解析已在路上飞奔，马上就到！
知识点
17．已知函数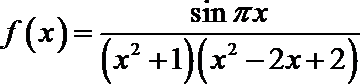
① 函数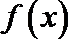
② 函数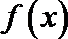
③ 函数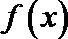
④对于任意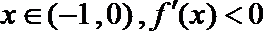
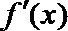
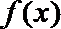
其中真命题的序号是（ ）．（填写出所有真命题的序号）
正确答案
②③
解析
解析已在路上飞奔，马上就到！
知识点
15．现有一个关于平面图形的命题：如图所示，同一个平面内的两个边长都是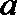
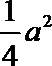
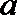
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．过点
（1）若抛物线在点
（2）过点
正确答案
（1） 设
由
则过点
由已知：
即点
（2）由已知，直线
联立
所以
解析
解析已在路上飞奔，马上就到！
知识点
18．一袋中装有分别标记着1，2，3，4数字的4只小球，每次从袋中取出一只球，设每只小球被取到的可能性相同.
（1）若每次取出的球不放回袋中，求恰好第三次取到标号为3的球的概率；
（2）若每次取出的球放回袋中，然后再取出一只球，现连续取三次球，若三次取出的球中标号最大的数字为
正确答案
（1）
（2）提示：
故
解析
解析已在路上飞奔，马上就到！
知识点
20．如图，五面体
（1）
（2）当
正确答案
（1）
当
证明:连结
∵四边形
∵
且
∴
∴
（2）
建立空间直角坐标系
则
所以
设
则有
即
令
法向量为
而平面
所以
所以二面角
解析
解析已在路上飞奔，马上就到！
知识点
19．在
（1）若
（2）若
正确答案
（1）由条件：
故
由
得
所以
（2）由余弦定理：
当且仅当
解析
解析已在路上飞奔，马上就到！
知识点
22．设函数
（1）若函数
（2）若函数
（3）若函数
正确答案
解：（1）
令
（2）
即
所以
（3）由①
①当
由题意知
存在这样的
②当
这时函数
由题意
即 
综合①②知：满足题意 
解析
解析已在路上飞奔，马上就到！