理科数学大庆市2014年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3．已知，为两条不同的直线,，为两个不同的平面,下列命题中正确的是（）

A,,且,则

B若平面内有不共线的三点到平面的距离相等,则

C若,则

D若,则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用空间中直线与平面之间的位置关系平面与平面之间的位置关系

题型：单选题

分值: 5分

7. 函数的最小正周期是，若其图象向右平移个单位后得到的函数为奇函数，则函数的图象（）

A关于点对称

B关于对称

C关于点对称

D关于对称

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的奇偶性函数y=Asin（ωx+φ）的图象变换由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

分值: 5分

1. 已知集合若,则为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

并集及其运算交集及其运算

题型：单选题

分值: 5分

2．设是虚数单位，若复数是纯虚数，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的基本概念复数代数形式的乘除运算

题型：单选题

分值: 5分

8. 若则的大小关系为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数幂的运算对数的运算性质对数值大小的比较

题型：单选题

分值: 5分

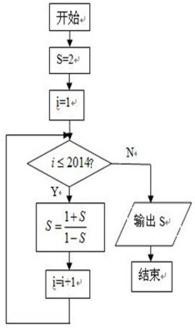
9. 程序框图如图所示，该程序运行后输出的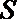的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

题型：单选题

分值: 5分

4．给出下列三个结论：

（1）若命题为假命题，命题为假命题，则命题“”为假命题；

（2）命题“若，则或”的否命题为“若，则或”；

（3）命题“”的否定是“ ”.

则以上结论正确的个数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断命题的真假判断与应用含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

分值: 5分

5.设等比数列中，前n项和为,已知，则（）

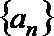
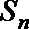
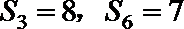
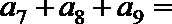
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用

题型：单选题

分值: 5分

6. 将4名实习教师分配到高一年级三个班实习，每班至少安排一名教师，则不同的分配方案有（）种

A12

B36

C72

D108

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

排列、组合及简单计数问题

题型：单选题

分值: 5分

10. 已知向量，，且，若实数满足不等式，则实数的取值范围为（）

A[－3,3]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

量积判断两个平面向量的垂直关系其它不等式的解法绝对值不等式的解法

题型：单选题

分值: 5分

11. 若抛物线上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质

题型：单选题

分值: 5分

12．已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积最大时，其高的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积与球体有关的内切、外接问题

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

14.某几何体的三视图如图，则它的体积是________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单空间图形的三视图棱柱、棱锥、棱台的体积

题型：填空题

分值: 5分

15．，则数列的前项和____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定积分裂项相消法求和

题型：填空题

分值: 5分

13. 的展开式的常数项为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

分值: 5分

16．过双曲线的左焦点，作倾斜角为的直线交该双曲线右支于点P，若且，则双曲线的离心率为________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

量积判断两个平面向量的垂直关系向量在几何中的应用双曲线的几何性质

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．某校学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：

（1）指出这组数据的众数和中位数；

（2）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”.求从这16人中随机选取3人，至多有1人是“极幸福”的概率；

（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记表示抽到“极幸福”的人数，求的分布列及数学期望．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

n次独立重复试验中恰好发生k次的概率离散型随机变量及其分布列、均值与方差茎叶图众数、中位数、平均数

题型：简答题

分值: 12分

19．如图，直三棱柱中,，，，,点在线段上．

（1）若是中点，证明∥平面；

（2）当时，求二面角的余弦值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质线面角和二面角的求法

题型：简答题

分值: 12分

20. 已知椭圆C：经过点，离心率，直线的方程为 .

（1）求椭圆C的方程；

（2）AB是经过右焦点F的任一弦（不经过点P），设直线与l相交于点M，记PA,PB,PM的斜率分别为，问：是否存在常数，使得？若存在，求出的值，若不存在，说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程圆锥曲线中的探索性问题

题型：简答题

分值: 12分

17．在中，角对边分别是，满足．

（Ⅰ）求角的大小；

（Ⅱ）求的最大值，并求取得最大值时角的大小．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用余弦定理平面向量数量积的运算

题型：简答题

分值: 10分

请从22~24题中任选一题作答

22.选修4—1几何证明选讲:

如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E，OE交AD于点F。

（I）求证：DE是⊙O的切线；

（II）若的值.

23.选修4—4:坐标系与参数方程

在极坐标系中，已知圆C的圆心，半径

（Ⅰ）求圆C的极坐标方程；

（Ⅱ）若，直线l的参数方程为（t为参数），直线l交圆C于A、B两点，求弦长|AB|的取值范围．

24.选修4—5:不等式选讲

已知函数。

（1）若的解集为，求实数的值。

（2）当且时，解关于的不等式。

正确答案

22.

23.

24.

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：简答题

分值: 12分

21. 已知函数，当时，有极大值。

（1）求实数的值；

（2）若存在，使得成立，求实数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷