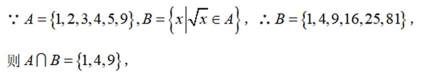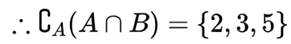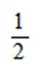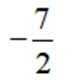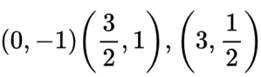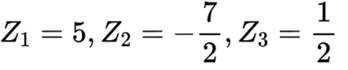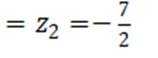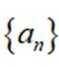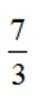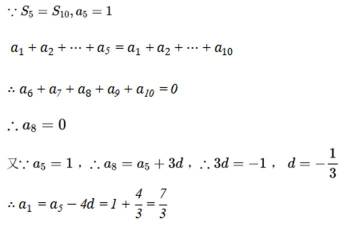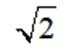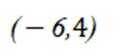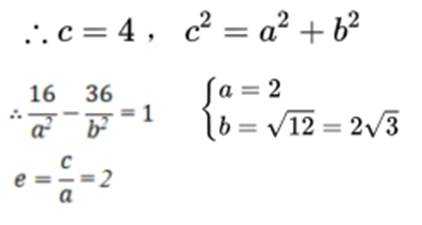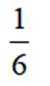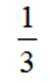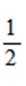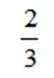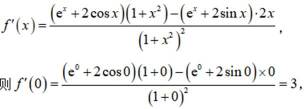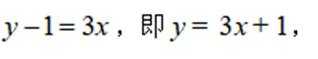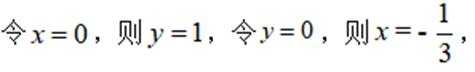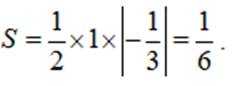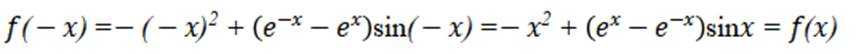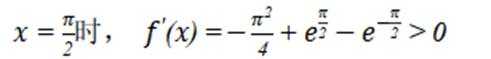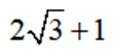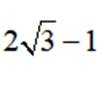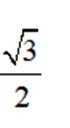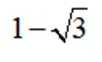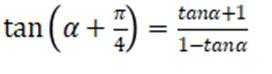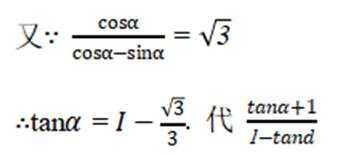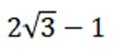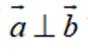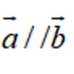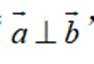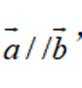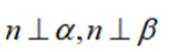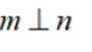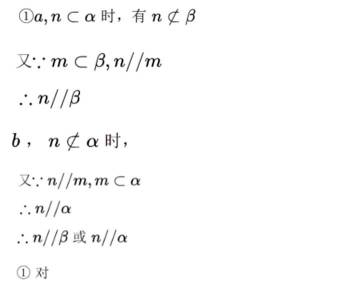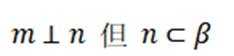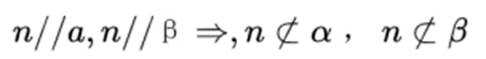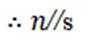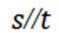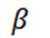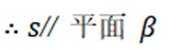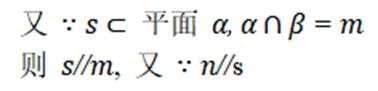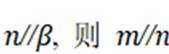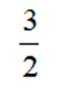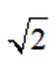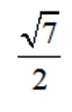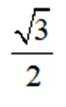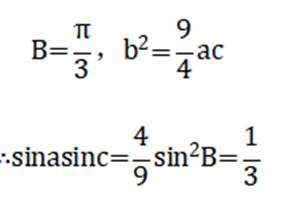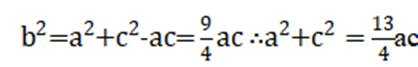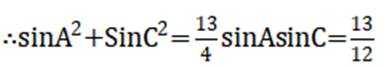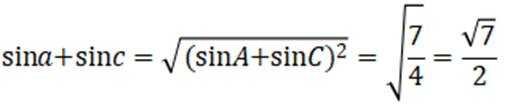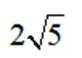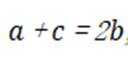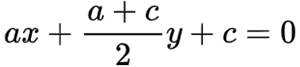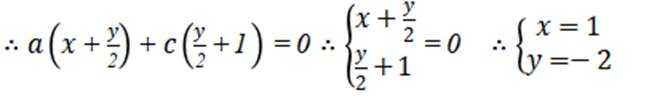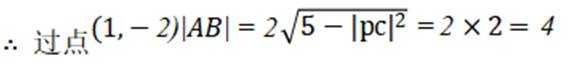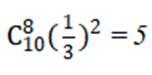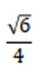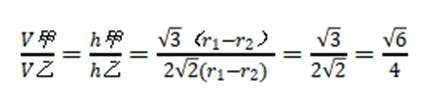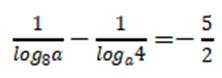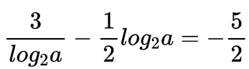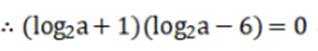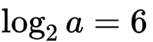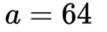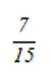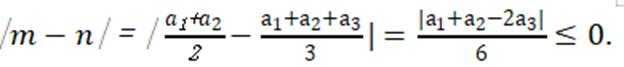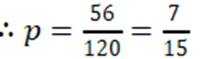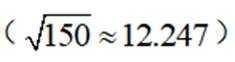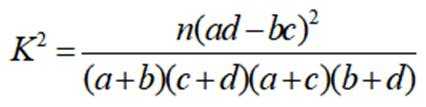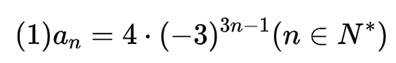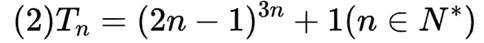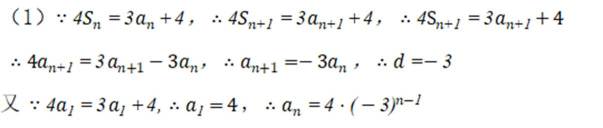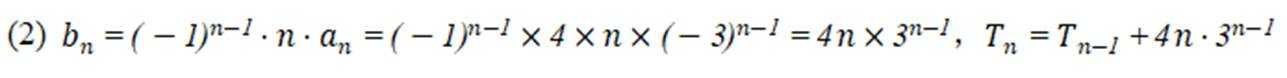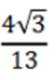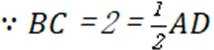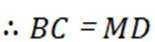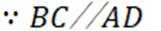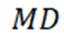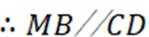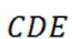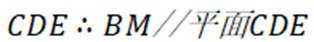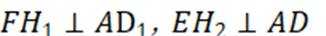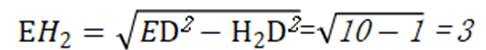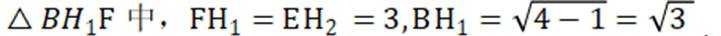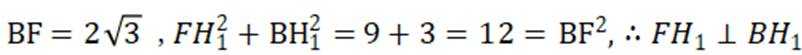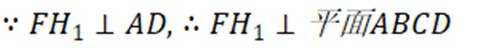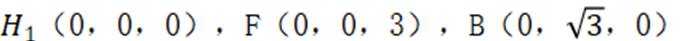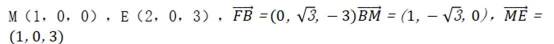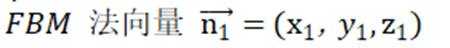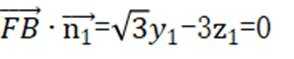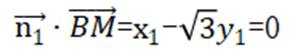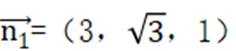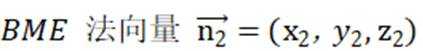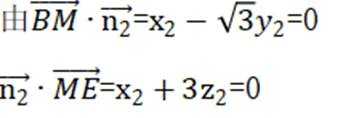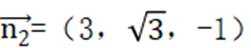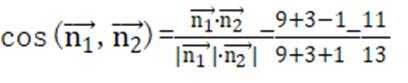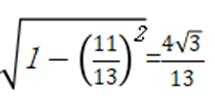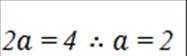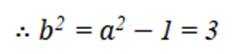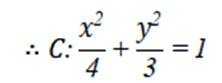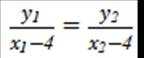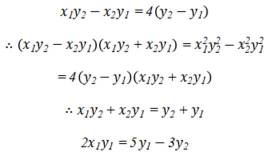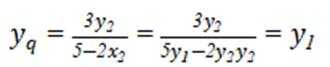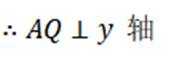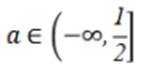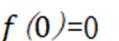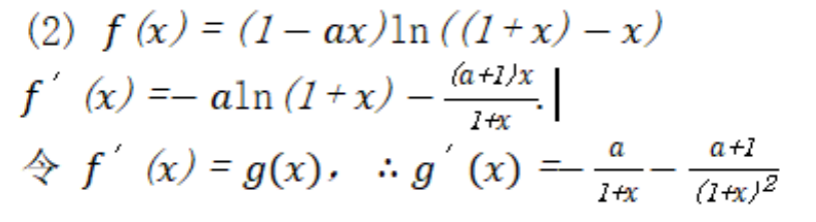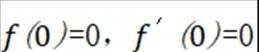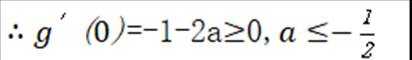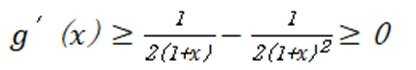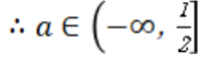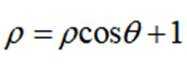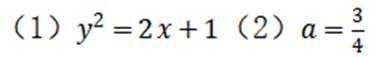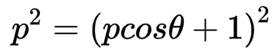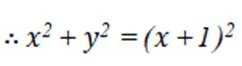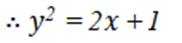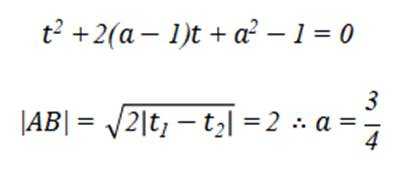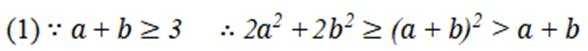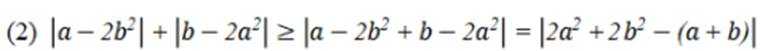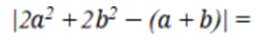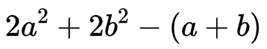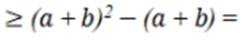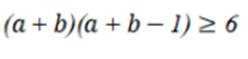- 真题试卷
- 模拟试卷
- 预测试卷
设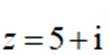
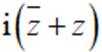
正确答案
解析
本题主要考查了复数的相关知识,包括复数的共轭复数、复数的四则运算等。
由题干可得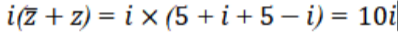
集合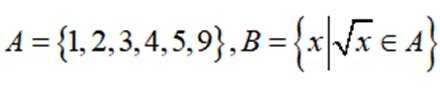
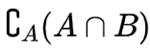
正确答案
解析
本题主要考查了集合的基本运算,包括交集、补集,同时还涉及到对集合中元素的分析,以及根据条件确定集合的具体内容。
由题意知:
故选D.
若实数X,Y满足约束条件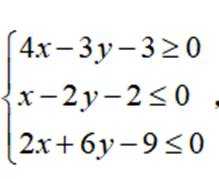
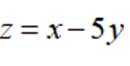
正确答案
解析
本题主要考查了线性规划的知识点。线性规划是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
联立约束条件,得
代入函数
故选D.
等差数列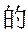
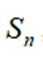
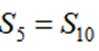
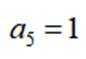
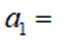
正确答案
解析
本题主要考查了等差数列的性质、前n项和公式等知识点。
已知双曲线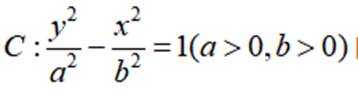
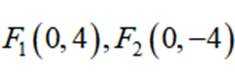
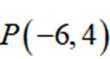
正确答案
解析
本题主要考查了双曲线的定义、性质,包括焦点的位置和距离关系以及点与双曲线的位置关系等知识点。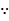
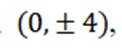
设函数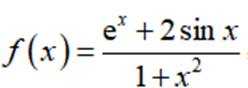
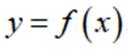
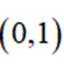
正确答案
解析
本题主要考查了导数的几何意义,通过求函数的导数来得到曲线在某一点的切线斜率,同时还涉及到三角形面积的计算。
即该切线方程为
故该切线与两坐标轴所围成的三角形面积
故选:A.
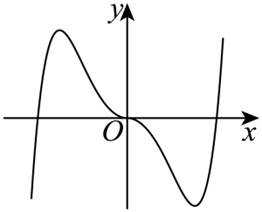
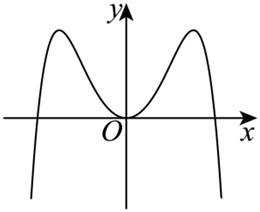
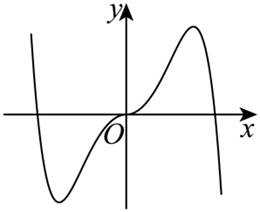
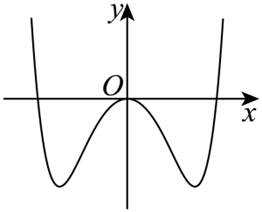
函数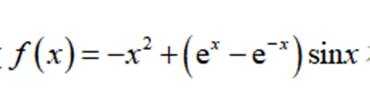
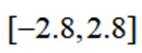
正确答案
解析
本题主要考查了函数的性质,包括奇偶性、单调性等,还涉及到一些基本函数的图像特征。
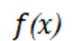
故排除 D项,选择B
已知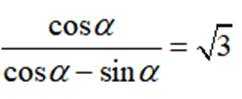
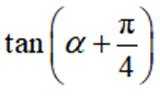
正确答案
解析
本题主要考查了三角函数的弦化切以及两角和的正切公式这两个知识点。
得
已知向量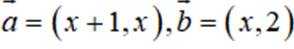
正确答案
解析
本题主要考查了向量垂直和平行的条件,以及充分条件和必要条件的判断同时还涉及到对充分条件和必要条件概念的理解和运用。
对A,当
所以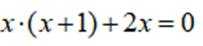
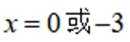
对C,当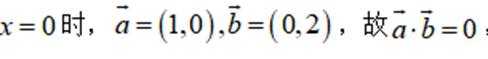
所以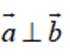
对B,当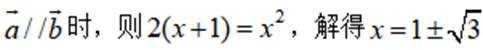
对D,当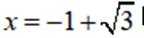
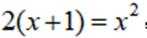
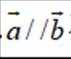
故选:C.
设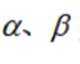
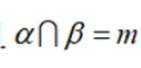
①若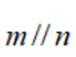
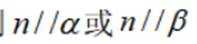
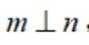
③若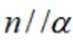
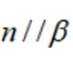
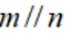
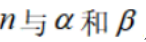
其中所有真命题的编号是( )
正确答案
解析
本题主要考查了直线与平面的位置关系,包括直线与平面平行、垂直的判定和性质,以及线线角,线面角等相关知识点。
②
如上图,
②错
即: 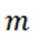
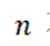
过 n, 分别作平面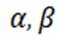
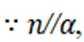
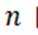
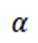
同理: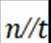
又 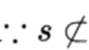
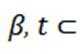
③对
④若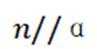
④错
11. 在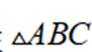
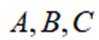
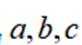
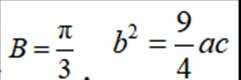
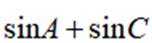
正确答案
解析
本题主要考查了正弦定理、余弦定理的应用,同时还涉及到三角函数的一些基本运算和性质。
已知b是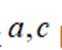
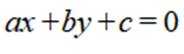
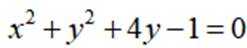
正确答案
解析
本题主要考查了等差中项的概念、直线与圆的位置关系、点到直线的距离公式等知识点。
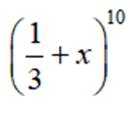
正确答案
5
解析
本题主要考查了二项式定理的相关知识。
最大值
已知甲、乙两个圆台上、下底面的半径均为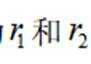
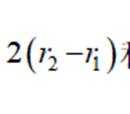
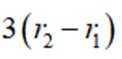
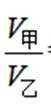
正确答案
解析
本题主要考查了圆台的结构特征圆台体积公式的应用。
已知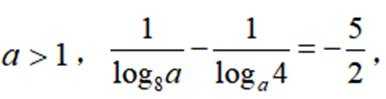
正确答案
64
解析
本题主要考查了对数的运算性质以及换元法的应用。
又因为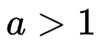
所以
有6个相同的球,分别标有数字1、2、3、4、5、6,从中不放回地随机抽取3次,每次取1个球.m为前两次取出的球上数字的平均值,n为取出的三个球上数字的平均值,则m与n差的绝对值不超过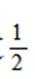
正确答案
解析
本题主要考查了概率的计算,以及对平均值概念的理解和运用,同时还涉及到分类讨论的思想。
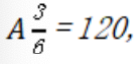
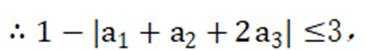
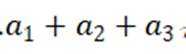
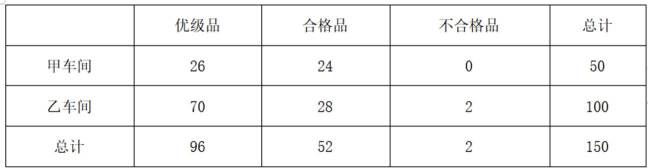
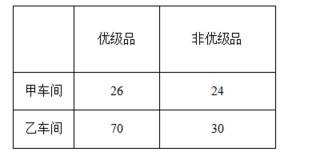
某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
(1)填写如下列联表:

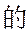
(2)已知升级改造前该工厂产品的优级品率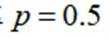
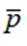
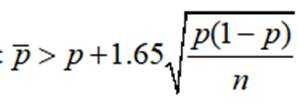
附:
正确答案
(1)没有99%的把握;(2)能
解析
本题主要考查了统计与概率的相关知识,根据题意可得列联表:
可得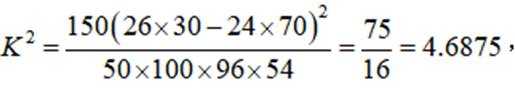
因为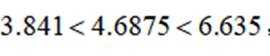
所以有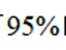

(2)由题意可知:生产线智能化升级改造后,该工厂产品的优级品的频率为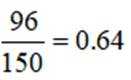
用频率估计概率可得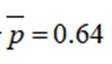
又因为升级改造前该工厂产品的优级品率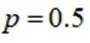
则
可知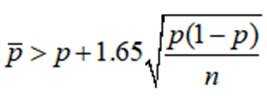
所以可以认为生产线智能化升级改造后,该工厂产品的优级品率提高了.
记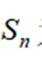
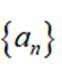
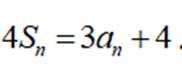
(1)求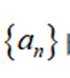
(2)设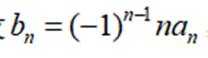
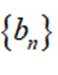
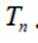
正确答案
解析
本题主要考查了数列的通项公式与前n项和的关系,等比数列的定义及通项公式,以及差比数列的求和方法等知识点。
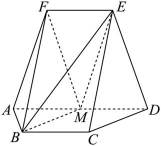
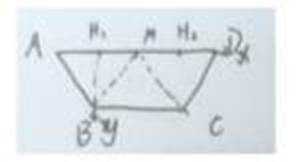
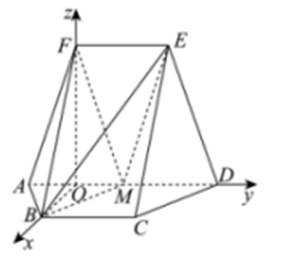
如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等腰梯形,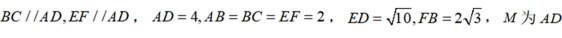
(1)证明: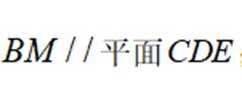
(2)求二面角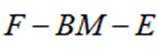
正确答案
(1)略(2)
解析
本题主要考查了空间直线与平面的位置关系、空间向量的应用、二面角等知识点。
(1)
又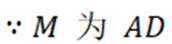
又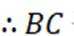
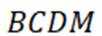
又 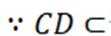
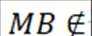
(2)底面图如下
在等腰梯形 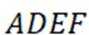
分别过 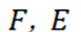
垂足为 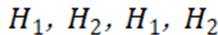
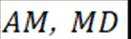
在 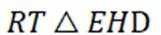
在
又
分别以 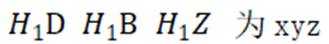
所示的空间直角坐标系
则
设平面
由
取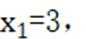
同理设平面
取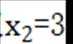
正弦值
设椭圆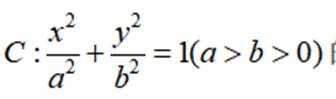
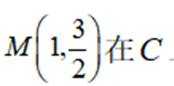
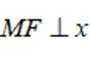
(1)求C的方程;
(2)过点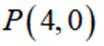
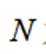

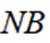
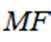
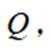
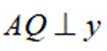
正确答案
(1)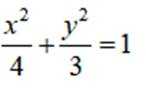
解析
本题主要考查了椭圆的标准方程、椭圆上的点的坐标特征、直线与椭圆的位置关系、中点坐标公式等知识点。
(1)
(2) 设 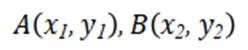
即
则
已知函数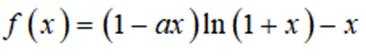
(1)当a=-2时,求f(x)的极值;
(2)当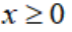
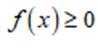
正确答案
(1)极小值为0,无极大值 (2)
解析
本题主要考查了函数的极值、导数的应用、不等式恒成立问题等知识点。
(1)当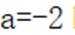
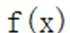
当 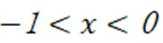
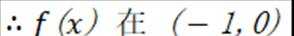
在 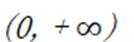
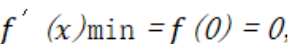
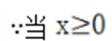
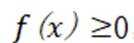
当 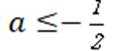
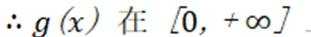
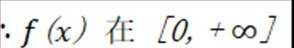
选考题:在平面直角坐标系
(1)写出C的直角坐标方程;
(2)设直线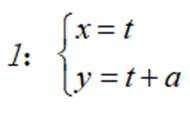
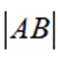
正确答案
解析
本题主要考查了极坐标方程与直角坐标方程的转化,以及直线参数方程的应用。
(1)
(2)将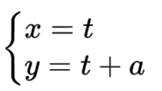
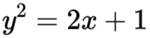
选考题:实数a,b满足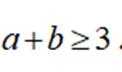
(1)证明: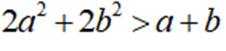
(2)证明: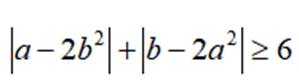
正确答案
(1)略(2)略